Question #506c8
1 Answer
The difference in the energy levels of the electrons is equal to the energy of the photon emitted.
Explanation:
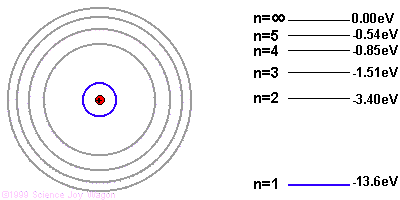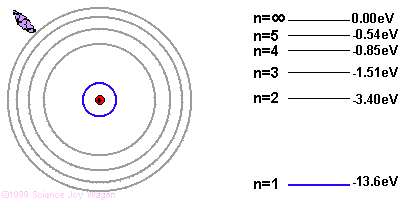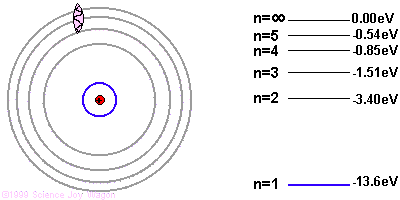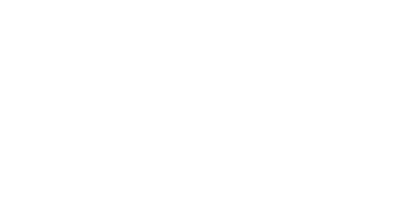
It's easiest to understand photon emission starting with the Bohr model of the atom. The Bohr model illustrates electron orbitals as rings around the nucleus, similar to the planets orbits around the sun. The farther the electron is from the nucleus, the higher the electron's energy level.
 http://www.regentsprep.org/regents/physics/phys05/catomodel/bohr.htm
http://www.regentsprep.org/regents/physics/phys05/catomodel/bohr.htm
Due to quantum mechanics, the electrons are only allowed to have specific energies when they are part of the atom. They can jump from one energy level to the next, but they cannot be in between energy levels.
If the electron starts in a higher energy orbital farther from the nucleus, and moves to a lower energy orbital closer to the nucleus, the atom loses energy. The first law of thermodynamics says that energy has to go somewhere, so the atom emits a photon of light with energy equal to the amount the atom lost.
Since the Planck constant,
 http://www2.astro.psu.edu/users/caryl/a10/lec6_2d.html
http://www2.astro.psu.edu/users/caryl/a10/lec6_2d.html
Each color in an emission spectrum represents an electron moving between two orbitals. The closer to the red side, the longer the wavelength, and therefore, the smaller the transition. The closer the line is to the blue side, the shorter the wavelength, and the larger the transition.

