Question #ba0bf
3 Answers
See the solution below.
Explanation:
Assuming that there is no drag experienced by the ski jumper. Also assume that Cartesian coordinate system has its origin at the point when jumper leaves the ramp.
At the time of jump, the ski jumper has given velocity
It has two components
It is clear that initially he will rise up and then start falling down due to action of gravity. The acceleration due to gravity
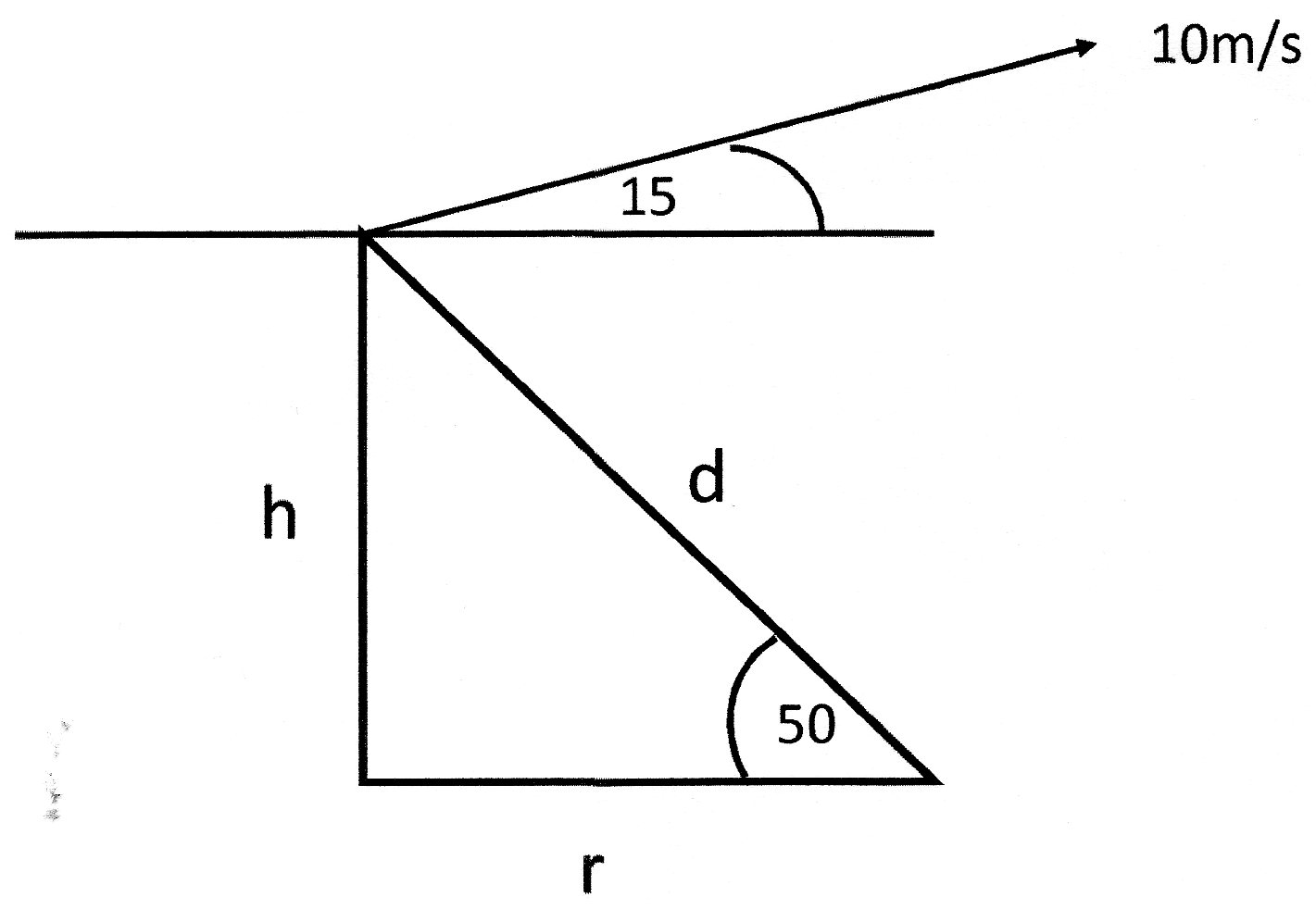
(a) Imagine a right angled triangle where
Hence
(b) The
Inserting the
Inserting value of sin of the angle from the table
There is no change in the
d=48.051 meters
Explanation:
a)
b)
(a)
(b)
Explanation:
(a)
The key to these projectile problems is to treat the vertical and horizontal components of the motion separately and use the fact that they share the same time of flight.
Fig 1
 MFDocs
MFDocs
I will use the vertical and horizontal components to eliminate
Then by simple trigonometry I will find
Considering the vertical component I will use:
I will use the convention that "up" is -+ve.
This becomes:
Considering the horizontal component, for which the velocity is constant, we can write:
From the geometry of the system we can also write:
Now we can set about eliminating
From
From
Combining these we get:
We can now substitute this value of
This is a quadratic equation for which:
Ignoring the zero root:
The minus sign signifies the downward direction.
From fig.1 we can say that:
(b)
For the horizontal component of velocity:
For the vertical component we can use:
This becomes:


