Question #ee73c
1 Answer
Here's what I got.
Explanation:
!! LONG ANSWER !!
Ok, here's my take on this. The way I see it, you are actually supposed to determine the molecular mass of the compound, not its molecular formula.
In order to calculate its molecular formula you need to have some information about its percent composition. This will allow you to find its empirical formula first, then use its molecular mass to find its molecular formula.
Also, I am not really sure what aqueous tension means, although I do suspect that it's actually the vapor pressure of water vapor at that temperature, i.e.
http://www.endmemo.com/chem/vaporpressurewater.php
So, the idea here is that this problem is probably based on a Victor Meyer experiment, a laboratory technique used to find the molecular mass of a volatile compound.
The working principle revolves around the idea that the vapor of the unknown compound will displace an equal volume of dry air, which is then collected over water forming wet air.
A Victor Meyer apparatus
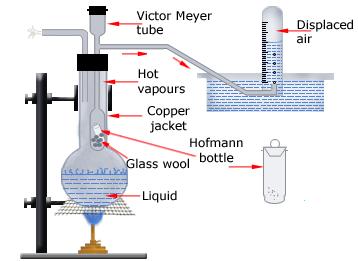
Your ultimate goal here will be to find the number of moles of your unknown substance present in the volume of vapor that displaced the dry air, not the wet air.
The easiest way to do that is to use the molar volume of a gas at STP. More specifically, you know that one mole of any ideal gas occupies exactly
- a pressure of
#"100 kPa"# - a temperature of
#0^@"C"#
The first important thing to keep in mind here is that air collected over water is actually a mixture of dry air, which is what was displaced by the vapor of your substance, and water vapor.
This means that the pressure of wet air will be
#P_"wet air" = P_"dry air" + P_"water vapor"#
The partial pressure of dry air will be, using the vapor pressure of water at
#P_"dry air" = "725 mmHg" - overbrace("12 mmHg")^(color(purple)("vapor pressure of water")) = "713 mmHg"#
Now, you know that the substance displaced a volume of
#color(blue)((P_1V_1)/T_1 = (P_2V_2)/T_2)#
Do not forget to use matching units for this! Also, the temperature must be expressed in Kelvin! Rearrange the equation to solve for
#V_2 = P_1/P_2 * T_2/T_1 * V_1#
You can go from mmHg to kPa by going through atm first.
#713 color(red)(cancel(color(black)("mmHg"))) * (1color(red)(cancel(color(black)("atm"))))/(760color(red)(cancel(color(black)("mmHg")))) * "101.325 kPa"/(1color(red)(cancel(color(black)("atm")))) = 711/760 * "101.325 kPa"#
This means that you'll have
#V_2 = (713/760 * 101.325 color(red)(cancel(color(black)("kPa"))))/(100color(red)(cancel(color(black)("kPa")))) * ((0 + 273.15)color(red)(cancel(color(black)("K"))))/((273.15 + 14)color(red)(cancel(color(black)("K")))) * "24.2 cm"^3#
#V_2 = "21.883 cm"^3#
So, your unknown substance displaced
#V_"substance" = V_"dry air" = "21.883 cm"^3#
The number of moles of your substance present in
#"21.883 cm"^3 = "21.883 mL"#
of vapor at STP will thus be
#21.883 color(red)(cancel(color(black)("mL"))) * (1 color(red)(cancel(color(black)("L"))))/(10^3color(red)(cancel(color(black)("mL")))) * overbrace("1 mole"/(22.7color(red)(cancel(color(black)("L")))))^(color(purple)("molar volume of a gas")) = "0.00096401moles"#
The molecular mass of a substance, which tells you the mass of one mole of that substance, can be calculated by dividing the mass of a sample by the number of moles it contains
#color(blue)("molar mass" = M_M = "mass"/"no. of moles" = m/n = ["grams"/"mol"])#
In your case, the sample had a mass of
#M_M = "0.188 g"/"0.00096401 moles" = color(green)("195 g/mol")#
I'll leave the answer rounded to three sig figs.
SIDE NOTE Many textbooks and online resources still list STP conditions as a pressure of
Under these conditions, one mole of any ideal gas occupies

