Question #45625
1 Answer
First, let's consult the chemistry explanation behind this, before we approach any mathematics: this ought to improve your understanding of the concept of the mole, that will help your thinking in the future.
First off, we should say this: the mole is just a number. Just as I may ask for a dozen eggs (with a "dozen" being a more conventional way of saying "twelve eggs," of course), I may similarly ask for a mole of eggs. Just as a dozen of eggs is twelve eggs, a mole of eggs is the Avogadro's number of eggs:
This number has not been randomly picked up out of thin air: it has been empirically (experimentally) determined that if I have a mole of a given element, its mass will be equal to its relative atomic mass (
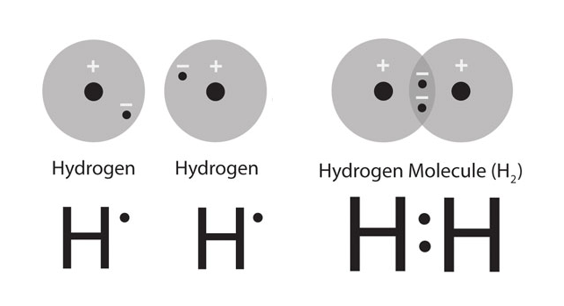
Recall that the element hydrogen goes around in pairs: it is a diatomic molecule (consult the resources on molecular orbital theory if you would like to understand why). So it is important when you're reading the periodic table that you take these sorts of things into account: in this case, if you were to use the data that
So right now we understand that when a sample of a substance has a mass equal to its respective relative mass, we must have one mole of that substance. We also know that hydrogen is a diatomic molecule, and that
And of course it is obvious now that this is a rather pleasant example. But what happens when you get some nasty data? It's not natural to assume that we will always be working with data like this. So make sure you're aware of the relationship between moles, mass, and relative mass using the equation below.
And in conclusion, our data will also confirm our deduction even in this case:
But in fact hydrogen has a slightly higher


