Question #5feb3
2 Answers
A) see below for rational
Explanation:
Since
A) They are parallel to each other
Explanation:
If, by hypothesis, (A) is true, then
- (B) must be false (because parallel lines are at an angle of
0^@ to each other and perpendicular lines are at an angle of90^@ to each other; - (C) must be false (because parallel lines never meet);
- (D) must be false (because skew lines have no intersections, but aren't parallel, they are in different planes).
So, if the hypothesis (A) is true, the other hypotheses are false.
Parallel lines are coplanar lines that do not intersect.
Therefore all the points of 2 parallel lines are coplanar.
Since line GE intercept the parallel lines AB and CD these 3 lines are coplanar (they are in the same plane).
Since line HF intercept the parallel lines AB and CD these 3 lines are coplanar (they are in the same plane).
If line GE is in the same plane defined by lines AB and CD and line HF is in the same plane as AB and CD, it means that lines GE and HF are coplanar.
Now consider the figure below
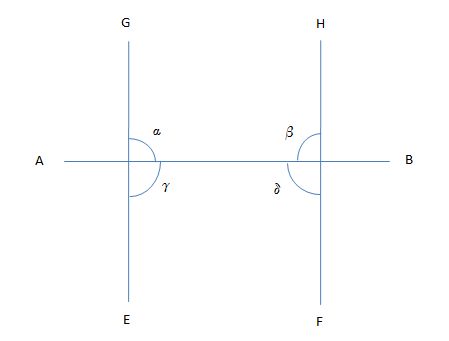 I created this figure using MS Excel
I created this figure using MS Excel
Counterproof using Euclidean Theorem I,17:
In any triangle the sum of any two angles is less than two right angles.
Euclid's Elements, Book I, Proposition 17
GE and HF are perpendicular to AB, it means that
alpha+beta=180^@ => in the half-plane above AB, there's no triangle defined by the intercepts of lines AB, GE and HF, because GE and HF don't meet;
gamma+delta=180^@ => in the half-plane below AB, there's no triangle defined by the intercepts of lines AB, GE and HF, because GE and HF don't meet.
-> Coplanar lines that never meet are parallel.
Direct proof using Euclidean Theorem I,27:
If a straight line falling on two straight lines makes the alternate angles equal to one another, then the straight lines are parallel to one another.
Euclid's Elements, Book I, Proposition 27
Since
alpha=delta=90^@
and
gamma=beta=90^@
-> GE and HF are parallel.


