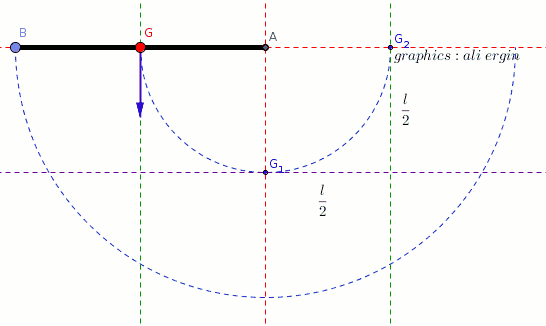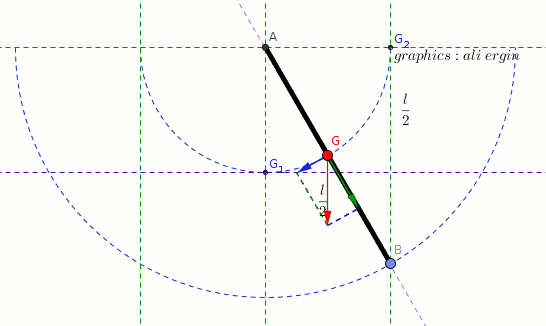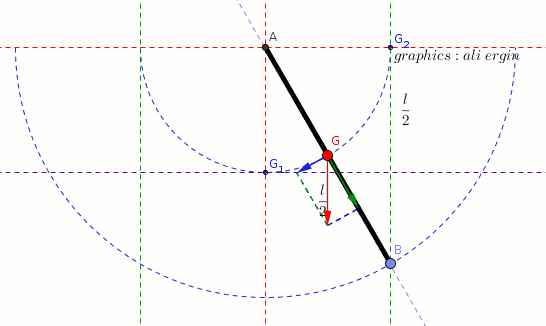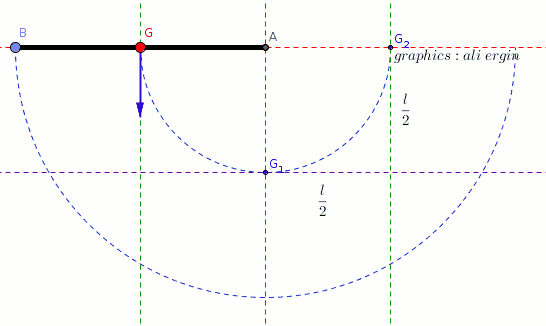
#"it will gain a potential energy if object is brought at horizontal position."#
#E_p=m*g*h#
#m:"mass of object"#
#g:"acceleration of gravity"#
#h=l/2#
#E_p=m*g*l/2#
#"it will turn and will gain a kinetic energy if object is released"#
#E_k=1/2*I*omega^2#
#I " represents the moment of inertia of rod"#
#omega" represents angular velocity of object"#
#"we can write "E_p=E_k " because Energy is reserved."#
#m*g*l/cancel(2)=1/cancel(2)*I*omega^2#
#m*g*l=I*omega^2#
#" so " I=1/3*m*l^2" (moment of inertia for a rod turning its one end)"#
#"we can write as:"#
#cancel(m)*g*cancel(l)=1/3*cancel(m)*cancel(l^2)*omega^2#
#g=1/3l*omega^2#
#omega^2=(3g)/l#
#sqrt(omega^2)=sqrt((3g)/l)#
#omega=sqrt((3g)/l)#

