Question #96821
1 Answer
Here's how you can do that.
Explanation:
Packing efficiency is all about how much space is being occupied by the atoms present in a unit cell.
In order to calculate packing efficiency, you basically need to know three things
- how many atoms you get per unit cell
- the volume of a single atom
- the total volume of the unit cell
Packing efficiency will be equal to
#color(blue)(|bar(ul(color(white)(a/a)"pack. eff." = "volume occupied by atoms"/"total volume of the unit cell"color(white)(a/a)|)))#
So, start by calculating how many atoms you get in a hexagonal closed-packed (HCP) unit cell.
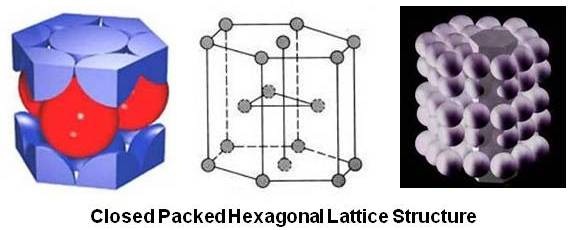
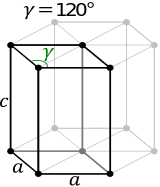
A HCP unit cell is a hexegonal prism that has a total of
- three lattice points in the center of the cell
- two lattice points in the centers of the bases
- twelve lattice points in the corners of the unit cell
Now, take a look at how the atoms are packed in the unit cell. Notice that you have
#1# atom for every lattice point located in the center of the unit cell#1/2# of an atom for every lattice point located in the center of the two bases#1/6"th"# of an atom for every lattice point located in the corners of the unit cell
The total number of atoms that can fit in a HCP unit cell will thus be
#3 xx "1 atom" + 2 xx 1/2color(white)(a)"atoms" + 12 xx 1/6color(white)(a)"atoms" = "6 atoms"#
At this point, it would be easier to work with a primitive unit cell, which is equivalent to
Projecting this primitive cell here will get you
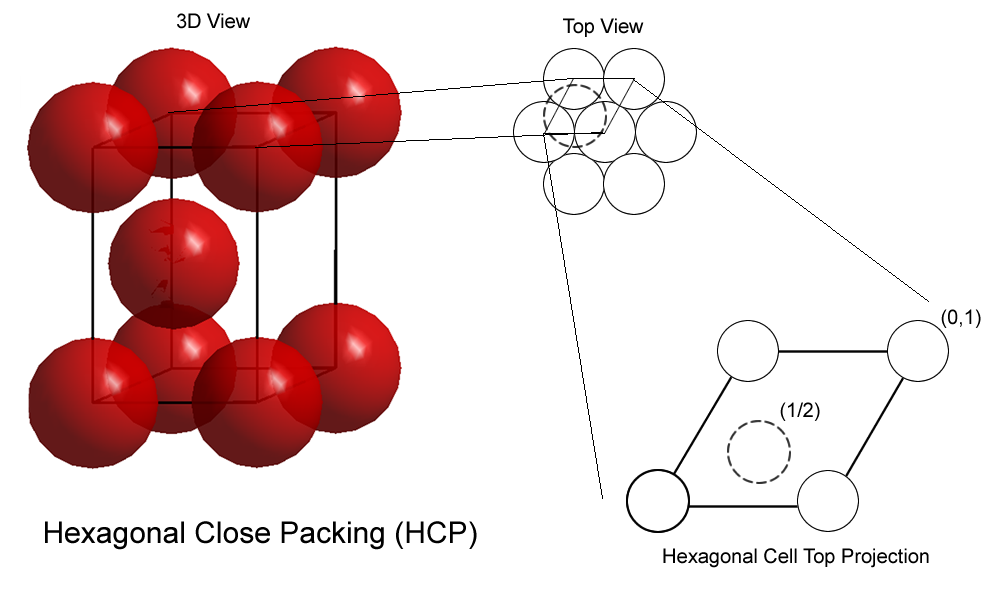
This primitive unit cell will contain
#a = 2r implies r = a/2" " " "color(orange)("(*)")#
Here
Now, to get the volume of this primitive cell, you must use a known relationship that exists between the length of the cell and it height, usually given as
More specifically, you can use the fact that
#color(purple)(|bar(ul(color(white)(a/a)color(black)(c = sqrt(8/3) * a = (2sqrt(6))/3 * a)color(white)(a/a)|)))#
The volume of this primitive unit cell will thus be equal to the area of the rhombus that makes up its base and the height of the cell. Now the area of a rhombus can be expressed using the length of its side and an interior angle.
http://www.mathwords.com/a/area_rhombus.htm
#"area rhombus" = a^2 * sin(A)#
In your case, you can say that
#"area rhombus" = a^2 * sin(120^@) = sqrt(3)/2 * a^2#
SIDE NOTE This will of course be equivalent to
#"area rhombus" = a^2 * sin(60^@) = sqrt(3)/2 * a^2#
The volume of the primitive unit cell will thus be
#V_"primitive cell" = overbrace(sqrt(3)/color(red)(cancel(color(black)(2))) * a^2)^(color(green)("area of the rhombus")) xx overbrace((color(red)(cancel(color(black)(2)))sqrt(6))/3 * a)^(color(blue)("height of the cell"))#
#V_"primitive cell" = (sqrt(3) * sqrt(6))/3 * a^3 = sqrt(2) * a^3#
Since a primitive cell is equivalent to
#V_"unit cell" = 3 xx sqrt(2) * a^3 = 3sqrt(2) * a^3#
The volume of a single atom is given by
#color(purple)(|bar(ul(color(white)(a/a)color(black)(V_"atom" = 4/3 * pi * r^3)color(white)(a/a)|)))#
Use equation
#V_"atom" = 4/3 * pi * (a/2)^3#
#V_"atom" = 4/3 * pi * a^3/8 = pi/6 * a^3#
Since you know that you get
#V_"occupied" = color(red)(cancel(color(black)(6))) xx pi/color(red)(cancel(color(black)(6))) * a^3 = pi * a^3#
This means that the packing efficiency will be
#"pack. eff" = V_"occupied"/V_"unit cell"#
#"pack. eff" = (pi * color(red)(cancel(color(black)(a^3))))/(3sqrt(2) * color(red)(cancel(color(black)(a^3)))) = color(green)(|bar(ul(color(white)(a/a)0.7405color(white)(a/a)|)))#
You'll also see this expressed as percent packing efficiency
#"% pack. eff" = color(green)(|bar(ul(color(white)(a/a)74.05%color(white)(a/a)|)))#