Question #cec47
1 Answer
See explanation field below.
Explanation:
Let us first understand what is Angular Displacement
When a body is rotated about a specified axis, the angle of rotation of the radius vector or the distance moved by the body along the curved path is defined as its angular displacement.
The length of the arc of curved path is measured as an angle.
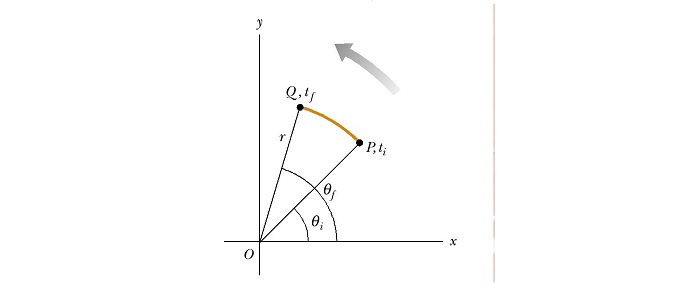
A point
At time
The angle moved by the radius vector is
Also,
Even though angular displacement is an entity with a direction and a magnitude it does not obey the commutative law for addition; for finite rotations. Therefore, it is not a vector.
For example addition and multiplication are commutative, but subtraction and division are not. Similarly, angular displacement is non-commutative.
