Question #54f82
1 Answer
Explanation:
Your strategy here will be to use Avogadro's number to convert the number of atoms of carbon to moles of carbon, then use the molecular formula of sucrose,
So, you know that you're dealing with a sample of sucrose that is known to contain
In order to convert this to moles of carbon, use the fact that a mole of atoms is defined as a collection of
#color(blue)(|bar(ul(color(white)(a/a)"1 mole atoms" = 6.022 * 10^(23)"atoms"color(white)(a/a)|)) ->)# Avogadro's number
You can say that the sample of sucrose contains
#4.897 * 10^(24)color(red)(cancel(color(black)("atoms"))) * "1 mole C"/(6.022 * 10^(23)color(red)(cancel(color(black)("atoms")))) = "8.132 moles C"#
Now that you know how many moles of carbon you have in your sample, use the fact that one molecule of sucrose contains
- twelve atoms of carbon,
#12 xx "C"# - twenty two atoms of hydrogen,
#22 xx "H"# - eleven atoms of oxygen,
#11 xx "O"#
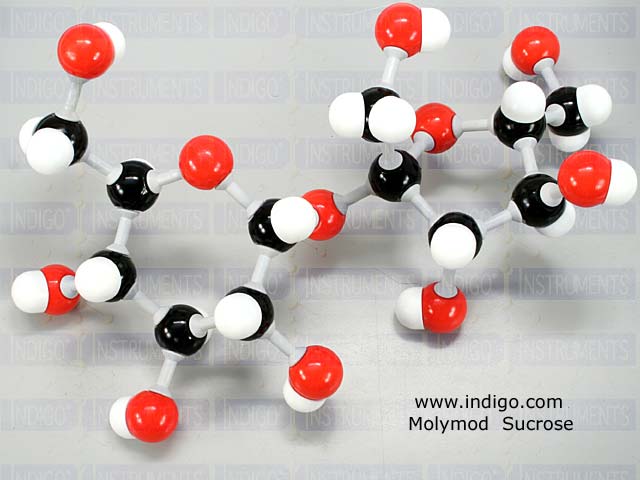
The carbon atoms are shown here in black, the oxygen atoms in red, and the hydrogen atoms in white.
So, if one molecule of sucrose contains
This means that the number of moles of carbon you have here will be enough to make up
#8.132 color(red)(cancel(color(black)("moles C"))) * "1 mole sucrose"/(12color(red)(cancel(color(black)("moles C")))) = color(green)(|bar(ul(color(white)(a/a)"0.6777 moles sucrose"color(white)(a/a)|)))#
The answer is rounded to four sig figs.

