Help me review kinetics??? I really don't get it and would appreciate a walkthrough of it!!
1 Answer
Alright, let's see. We'll be talking about:
- Rates of appearance (products) and disappearance (reactants)
- Rate laws and rate constants
- Collision theory and activation energy
- Reaction coordinate diagrams, activation energy, Gibbs' free energy, and catalysis
REACTION RATES
In general, a reaction will involve reactants and products. In accordance with conservation of mass and energy, the reactants will get used up while the products get created. This will occur over time.
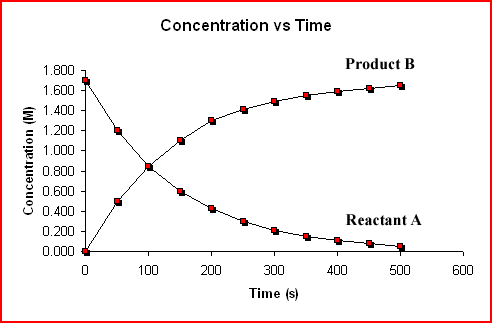
It is convenient to represent how quickly the reactants are used up and how quickly the products are made using a rate; specifically, some nice units are
In general, you write a rate as a function of time as:
#\mathbf(r(t) = -1/nu_R(d[R])/(dt) = 1/nu_P(d[P])/(dt))# where:
#+# indicates the appearance of product and#-# indicates the disappearance of reactant.#nu# is the stoichiometric coefficient in the balanced chemical reaction.#R# is any reactant, and#[R]# is the concentration of#R# in#"M"# , molarities.#P# is any product, and#[P]# is the concentration of#P# in#"M"# , molarities.#t# is time in#"s"# .
Let's say we had a hypothetical multi-step reaction with completely made up numbers:
#A + color(green)(2)B -> color(green)(2)C + color(green)(3)D#
So, the rates are written as:
#color(blue)(r(t) = -1/color(green)(1)(d[A])/(dt) = -1/color(green)(2)(d[B])/(dt) = 1/color(green)(2)(d[C])/(dt) = 1/color(green)(3)(d[D])/(dt))#
Remember, a rate just tells you the change in concentration over the change in time.
RATE LAWS AND RATE CONSTANTS
If you haven't seen this yet, you will eventually.
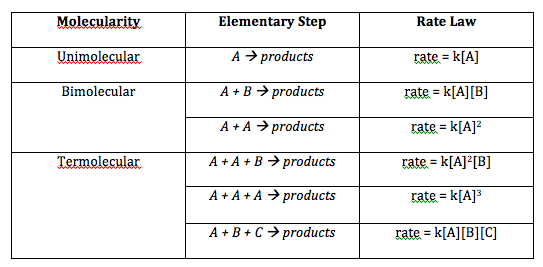
You can also have a rate law which relates a rate constant
#\mathbf(r(t) = k[A]^m[B]^n[C]^o[D]^p)#
#= \mathbf(-1/nu_A(d[A])/(dt) = - 1/nu_B(d[B])/(dt) = 1/nu_C(d[C])/(dt) = 1/nu_D(d[D])/(dt))# where:
#k# is the rate constant of the reaction, with units of#1/("M"^(1 -(m + n + o +p))cdot"s")# . The higher#k# is, the faster the reaction is.#m# ,#n# ,#o# , and#p# are different "orders" of the reactants involved. It basically tells you how much each reactant contributes to changing the rate of the reaction.
NOTE: The order does NOT correspond to the stoichiometric coefficient, or the denominator in the rate coefficient
As an example, let's say we had this classic, decomposition reaction:
#"N"_2"O"_4 -> color(green)(2)"NO"_2#
Then, its rate law (assuming a "first order" reactant), compiling all the information we just talked about, is:
#color(blue)(r(t) = k["N"_2"O"_4] = -1/color(green)(1)(d["N"_2"O"_4])/(dt) = 1/color(green)(2)(d["NO"_2])/(dt))#
Another question still remains: What makes a reaction occur? (Keep reading.)
COLLISIONS MUST OCCUR FOR A REACTION TO OCCUR
Collision theory is a qualitative description of how reactions occur. It essentially asserts that:
- All reactions require successful molecular collisions to occur (not all collisions are successful). That is, a molecule must fly into another one and cause a chemical change (like a bond breaking)!
- A successful collision is defined as one which gets the reactants over the energy barrier with activation energy
#E_a# . You gotta get the reactants riled up enough to react!
Some collisions are compared below of ethene (black/white) reacting with
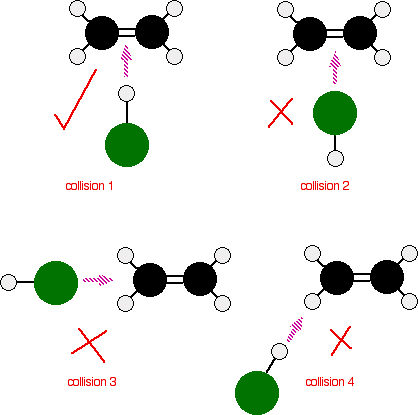
Basically, these aren't oriented correctly, except for collision 1. So, only collision 1 can be successful.
Okay, so now we have an idea of when a reaction can occur. What about tracing it while it occurs?
REACTION COORDINATE DIAGRAMS
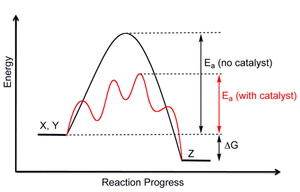
A reaction coordinate diagram tracks the progress of a reaction (its reaction coordinate), and indicates:
- Its activation energy
#E_a# , or the energy required for the reaction to occur. It's like trying to start a car and finally getting it to start---you've got over its activation energy. - Its change in Gibbs free energy
#DeltaG# going from reactants to products, which tells you the spontaneity of the reaction (#DeltaG < 0# is spontaneous, while#DeltaG > 0# is nonspontaneous;#DeltaG = 0# indicates equilibrium). This tells you whether the products are more stable (#DeltaG < 0# ) or less stable (#DeltaG > 0# ).
What you should notice from the diagram is that the activation energy decreases when you add a catalyst. That's because the catalyst introduces a new reaction pathway that requires less energy to occur.
This new reaction pathway might require more steps; the diagram above shows that, since we see the greater number of transition states and intermediates. The transition states are the peaks, and the intermediates are the wells.
For the diagram above, since

