For a tube open on both ends for fundamental frequency standing wave is so produced that there are Anti Nodes at both open ends and Node at the middle, as shown in the figure below.
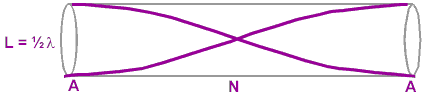
The wave length #lambda # of the fundamental and length #L# of the tube are related as
#L=lambda/2# ....(1)
We know that #v=nlambda#,
where #v# is velocity of sound in air, #n# is the frequency of the sound signal. Taking speed of sound in air as #343ms^-1#, we obtain
#343=390lambda#
or #lambda=343/390m#
Inserting in (1) we get
#L=343/(390xx2)#
#L=343/(780)m# ....(2)
Now #1/4# of the tube is immersed in water. The new length of air column is #3/4 xx " L#. Moreover now the tube is closed at one end and open at the other end. In this case we have Node at one end, water side and Anti Node at the other as shown in the picture below
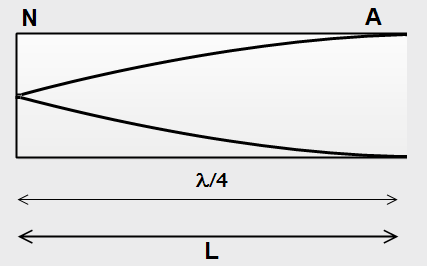
The new length #L_"new"=lambda_"new"/4# .......(3)
from #v=n_"new"lambda_"new"# we obtain
#n_"new"=v/lambda_"new"# .....(4)
From (2) we have
#L_"new"=3/4xx343/(780)#, inserting in (3)
#lambda_"new"=4xx3/4xx343/(780)=343/260#
From (4)
#n_"new"=343/(343/260)=260Hz#


