Why is entropy equal to #q# for a reversible process? What is the difference between reversible and irreversible?
1 Answer
Entropy is defined as
#\mathbf(DeltaS >= q/T),#
where the definition separates as
#DeltaS > (q_"irr")/T,#
#DeltaS = (q_"rev")/T,#
with
ENTROPY VS HEAT FLOW
By definition, entropy in the context of heat flow at a given temperature is:
The extent to which the heat flow affects the number of microstates a system can access at that temperature.
So, it's essentially a threshold for how significantly you can increase the dispersion of particle energy in a system by supplying heat into the system.
The higher the resultant entropy, the more influential the heat flow was, and the less heat you needed to impart into the system to get its energy distribution to a certain amount of dispersiveness.
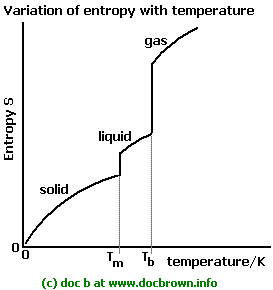
This should make sense if you compare the entropy of a gas to that of a liquid; a gas is more freely moving, so its energy can become more dispersed more easily.
(Same with a liquid vs. a solid.)
REVERSIBLE HEAT FLOW
Adding reversible heat
In other words, you're adding heat so slowly that the system has time to re-equilibrate as you add heat. This is basically the maximum amount of heat that you can add.
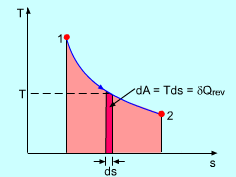
It's analogous to doing a full integral instead of doing an MRAM, RRAM, or LRAM approximation. You don't overestimate, underestimate, or miss anything.
You (ideally) retain all the heat that you add.
IRREVERSIBLE HEAT FLOW
Adding irreversible, inefficient heat
An example is adding heat, then pausing momentarily, then adding more heat in a separate, second step. This allows the system to lose heat while you are stopping momentarily.
You could infer from what I said earlier that it's like approximating (and underestimating) the area under the curve for the
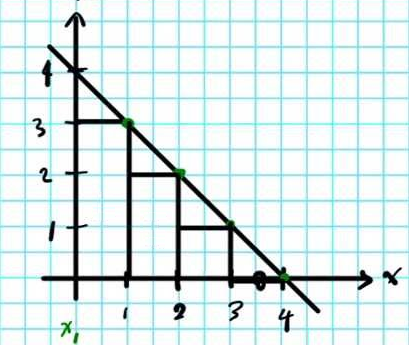
Since we know that some heat was lost when
This heat is represented by the unaddressed triangles in the above diagram. What we really get is:
#color(blue)(q_"irr" + q_"lost" = q_"rev")#
Thus,
Now compare back to the original expressions at the top of the answer, and you should convince yourself that this holds true.
WHY IS ENTROPY EQUAL TO REVERSIBLE HEAT FLOW?
Well, let's put it this way. If you do stuff in such a way that you go from an initial state back to a final state equal to the initial state, then you've performed a cyclic process (such as the Carnot cycle).
We denote this as
This makes sense, because we know that entropy is a state function, so if
#color(blue)(ointdS = DeltaS = 0).#
But if you perform an
That's not kosher, because
Hence, it couldn't be that
If you perform an
#color(blue)(oint_(S_i)^(S_f)dS = DeltaS = oint_(T_1)^(T_2) (deltaq_"rev")/TdT = 0)#

