Question #6bd6c
2 Answers
0
Explanation:
so
It could be the area, but the function does not maintain a constant sign between
Explanation:
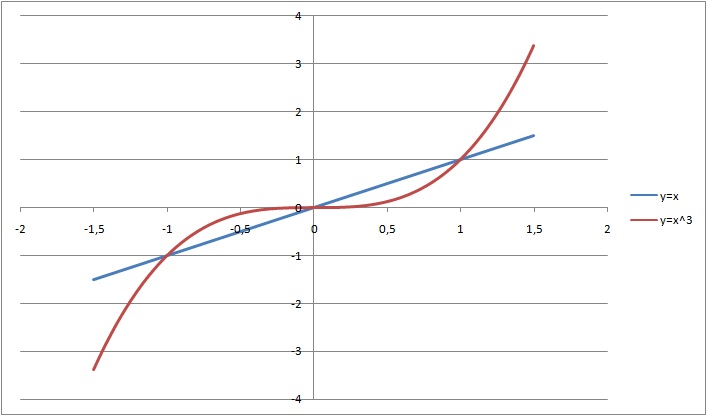
Geometrically, the integral of a function of only one variable equals to an area. However, the geometry suggests the that smaller valued function is substracted from the bigger valued function in order for the area to not be negative. More specifically, for two functions
That is, one must know which one of the following cases actually hold true:
Now considering your function, the find the sign of the difference between these functions:
We see that for the given area of
Since the area from 0 to 1 would be negative, we just add a minus sign so it adds up. If you solve the integrals:
Notice that the two integrals yield the same value? That's because of the symmetry of the function, which causes your integral to be negative.
To sum up:
Your integral is equal to:
The area of the function, if it was asked, would be:
Therefore, it may remind of area, but the integral you are given does NOT represent area (you could know this from the beginning, since an area can't be 0). The only geometrical result that could be obtained would be the symmetry of the function. For axis of symmetry