Question

Question #e29ae

Answer 1

`4.67`

Explanation:

The idea here is that you can use Graham's Law of Effusion to express the rate of effusion of hydrogen gas, `"H"_2`, relative to the rate of effusion of carbon dioxide, `"CO"_2`.

As you know, effusion is the process in which the molecules of a gas escape through a pinhole in their container.

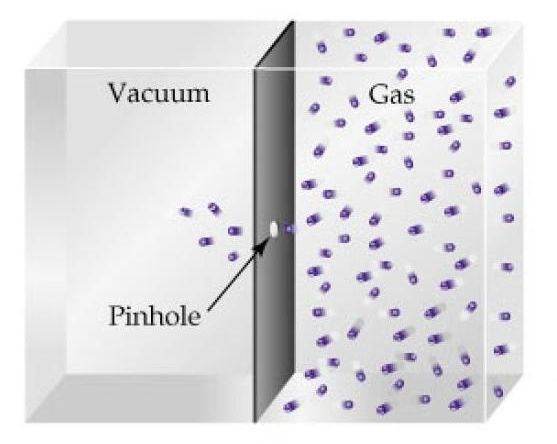
The rate of effusion essentially tells you the number of molecules of gas that escape through the pinhole per unit of time, usually per second.

According to Graham's Law, the rate at which a gas effuses is Inversely proportional to the square root of its molar mass

`color(blue)(|bar(ul(color(white)(a/a)"rate of effusion" prop 1/sqrt("molar mass")color(white)(a/a)|)))`

This means that heavier molecules will effuse slower than lighter molecules.

In your case, the rate of effusion of hydrogen gas relative to the rate of effusion of carbon dioxide can be expressed as

`"rate H"_ 2/"rate CO"_ 2 = 1/sqrt(M_("M H"_2)) * sqrt(M_("M CO"_2))`

`color(green)(|bar(ul(color(white)(a/a)color(black)("rate H"_ 2/"rate CO"_ 2 = sqrt( M_ ("M CO"_ 2)/M_ ("M H"_ 2)))color(white)(a/a)|)))`

Here

`M_ ("M CO"_ 2)` - the molar mass of carbon dioxide, equal to `"44.01 g mol"^(-1)`
`M_ ("M H"_ 2)` - the molar mass of hydrogen gas, equal to `"2.016 g mol"^(-1)`

All you have to do now is plug in these values to find

`"rate H"_ 2/"rate CO"_ 2 = sqrt( (44.01 color(red)(cancel(color(black)("g mol"^(-1)))))/(2.016color(red)(cancel(color(black)("g mol"^(-1)))))) = color(green)(|bar(ul(color(white)(a/a)4.67color(white)(a/a)|)))`

This means that hydrogen gas will effuse `4.67` times faster than carbon dioxide.

This means that in a given period of time, you can expect `4.67` times more molecules of hydrogen gas to escape through the pinhole in their container than molecules of carbon dioxide.