Question #664de
2 Answers
Selection of sign in front of any vector quantity depends on choice of the coordinate system and the origin.
Explanation:
Once the directions of unit vectors,
Usually for Projectile motion the origin and
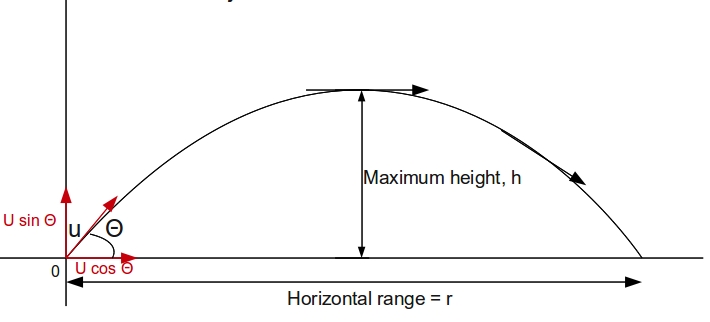
As gravity is acting against the
Similarly, when the projectile is falling down, its direction of motion is along
In case we shift the origin, to the point of maximum height, and redefine directions of
It isn't.
It is DOWN that's normally taken as negative (and up as positive).
Explanation:
Gravity is NOT necessarily negative.
It isn't necessarily positive.
What gravity is on earth is DOWN.
Towards the center of the earth.
It ends up as negative often because of a choice of
SIGN CONVENTION for a question (or a when building an equation). And it isn't JUST GRAVITY that ends up negative, every vector pointing down becomes negative.
When you're doing projectile motion near the earth's surface you treat the earth as flat (it isn't ), gravity as constant with height (it isn't) and the space as simple 3D space, up and down; north and south; and east and west. Each of these directions needs a SIGN CHOICE.
Take north as positive and south as negative;
Take east as positive and west as negative;
Take up as positive and down as negative.
You can pick other sign conventions (up as negative and down as positive) but once you pick a SIGN CONVENTION in a question you MUST STICK TO IT.
When you take DOWN as negative, (which is pretty standard) the sign of gravity becomes negative, but so does the sign of any downward displacement, velocity, acceleration, or force. It's not gravity that's negative, it's DOWN that's taken as negative.
Example Find the displacement of a skydriver after 5.0 s after jumping out of an airplane before his shoots opens, if his initial velocity from the push off is 2.00 m/s down.
We're taking DOWN as negative so
Negative means down! so in 5 second the skydriver has traveled 132.5 meters down.
or
We're taking DOWN as positive so
positive means down! so in 5 second the skydriver has traveled 132.5 meters down.
What matters is that the signs are consistent not which way they are.


