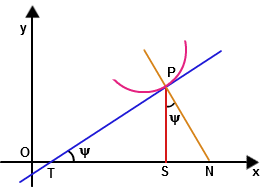
The subtangent is a segment #ST# on the X-axis from point #S#, an abscissa of some point #P# on a curve, to point #T#, intersection of a tangent to a curve at point #P# with the X-axis.
Knowing parametric expressions for #x=f(t)# and #y=g(t)#, for any parameter #t# we know abscissa and ordinate of a point #P(t)# on a curve.
In this case we will use ordinate #y=a(1-cos t)# and will determine #tan(Psi)#. That will be sufficient to find #ST#.
To calculate #tan(Psi)=dy/dx# we will use the property of parametric curve:
#dy/dx = (dy/dt)/(dx/dt)#
Using this approach,
#tan(Psi) = dy/dx = [a(sin t)]/[a(1+cos t)] = sin t/(1+cos t)#
Now we can calculate #ST#:
#ST = PS*tan(Psi) = y*dy/dx = a(1-cos t)*sin t/(1+cos t)#
This does not resemble any of the answers provided.
However, if #x=a(t-sin t)# then #dx/dt = 1-cos t# and answer #asin t# would be correct.


