Question #522dd
1 Answer
Explanation:
The magnetic orbital moment is given by
where
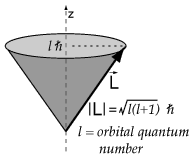
so the magnetic orbital moment is also 0
A unit of magnetic moment called the "Bohr magneton" is introduced here.
So the difference between them is
The magnetic orbital moment is given by
where

so the magnetic orbital moment is also 0
A unit of magnetic moment called the "Bohr magneton" is introduced here.
So the difference between them is