Question

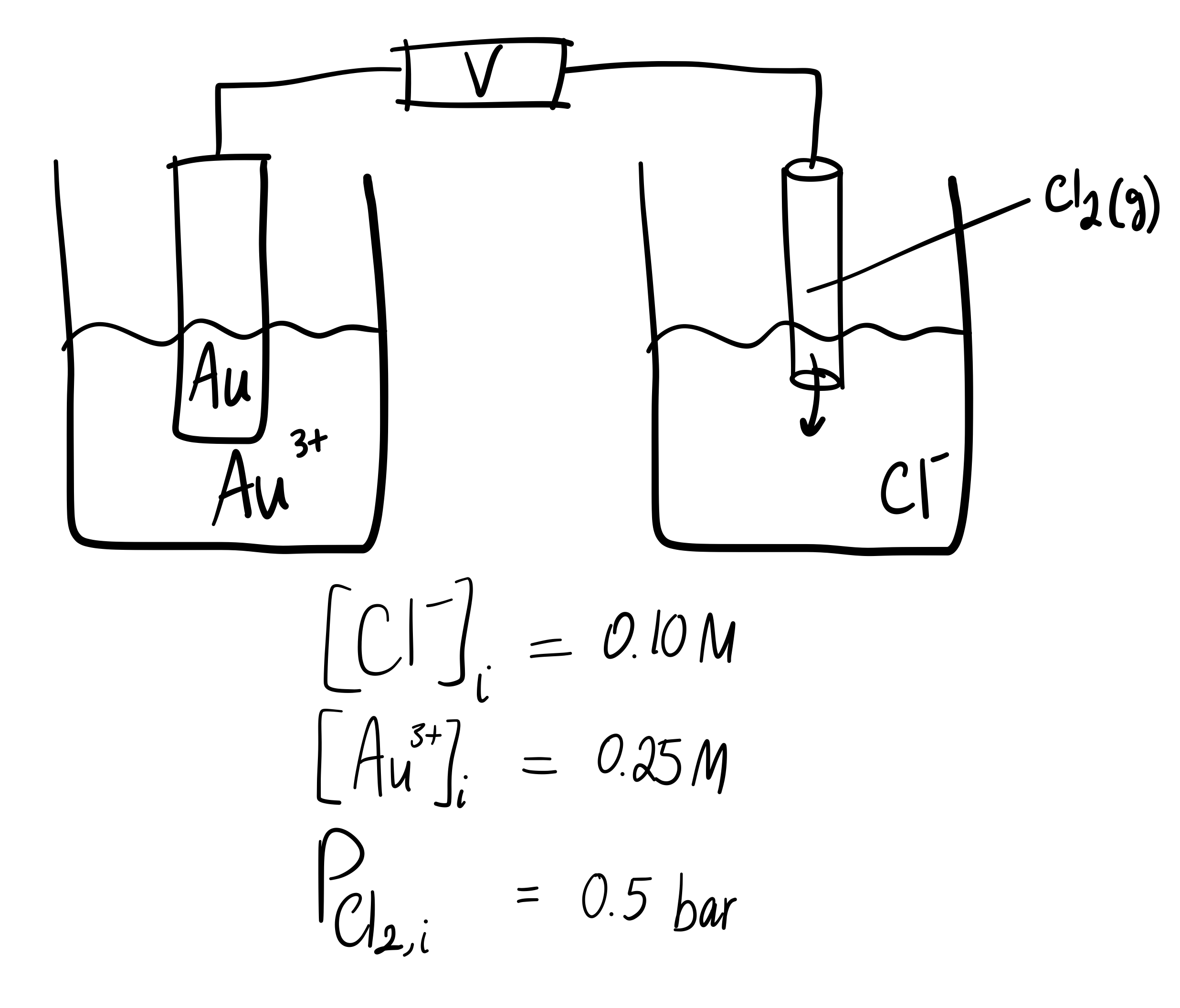
For the reaction of `"Au"^(3+)` with `"Cl"_2`, if `["Cl"^(-)]` and `["Au"^(3+)]` were initially `"0.10 M"` and `"0.25 M"` respectively, while `P_("Cl"_2) = "0.5 bar"` initially, what is `E_(cell)`?

Ecell=0.14V
Q=2x106
Ecell=0.07785V

Answer 1

Well, what I would do is draw out the problem to see what you got...

The Nernst equation is:

`E_(cell) = E_(cell)^@ - (RT)/(nF)lnQ`

• `E_(cell)` is the cell potential at nonstandard `T` and `P`. `""^@` signifies `"1 bar"` and `25^@ "C"`.
• `R` and `T` are known from the ideal gas law, and are in `"J/mol"cdot"K"` and `"K"`, respectively.
• `n` is the mols of electrons transferred in the overall reaction.
• `F = "96485 C/mol e"^(-)` is the Faraday constant.
• `Q` is the reaction quotient.

From the looks of it, you are supposed to calculate `E_(cell)` at this nonstandard, nonequilibrium state.

First, write out the half-reactions. You need to know how to look up reduction reactions in a standard reduction potential table, which is mandatory at any chemistry exam with electrochemistry questions.

`"Au"^(3+)(aq) + 3e^(-) -> "Au"(s)`, `" "E_(red)^@ = "1.50 V"`

`"Cl"_2(g) + 2e^(-) -> 2"Cl"^(-)(aq)`, `" "E_(red)^@ = "1.36 V"`

Since `E_(red)^@("Au") > E_(red)^@("Cl"_2)`, gold would rather be reduced than oxidized. Thus, the overall reaction at standard conditions is:

`2("Au"^(3+)(aq) + cancel(3e^(-)) -> "Au"(s))`, `" "E_(red)^@ = "1.50 V"`
`3(2"Cl"^(-)(aq) -> "Cl"_2(g) + cancel(2e^(-)))`, `" "E_(o x)^@ = -"1.36 V"`
`"-------------------------------------------"`
`2"Au"^(3+)(aq) + 6"Cl"^(-)(aq) -> 3"Cl"_2(g) + 2"Au"(s)`

And its standard cell potential, i.e. `E_(cell)^@` (and NOT `E_(cell)` as you had stated!) is:

`color(blue)(ul(E_(cell)^@)) = E_(red)^@ + E_(o x)^@`

`= "1.50 V" + (-"1.36 V") = ul(color(blue)(+"0.14 V"))`

For this reaction, we have the reaction quotient, which is written just like `K` but with current concentrations/partial pressures,

`Q = ((P_("Cl"_2(g))//P^@)^3)/((["Au"^(3+)(aq)]//c^@)^2(["Cl"^(-)]//c^@)^6)`

where `P^@ = "1 bar"` and `c^@ = "1 M"` such that `Q` is unitless. It must be, or else it cannot be operated on by `ln`.

We can immediately obtain the reaction quotient with the given data:

`color(blue)(ulQ) = ("0.5 bar"//"1 bar")^3/(("0.25 M"//"1 M")^2("0.10 M"//"1 M")^6)`

`= color(blue)(ul(2 xx 10^6))`

And that allows us to finally get the nonstandard cell potential. You didn't tell us the temperature, but I am guessing it is `"298.15 K"`.

`color(blue)(ul(E_(cell))) = "0.14 V" - (("8.314472 V"cdot"C/mol"cdot"K")("298.15 K"))/(("6 mol e"^(-)/("1 mol atom"))("96485 C/mol e"^(-)))ln(2 xx 10^6)`

`=` `"0.07787 V"`

`~~` `color(blue)(ul("0.07785 V"))`

And indeed it is at `"298.15 K"`. The answer wasn't exact because we were either using slightly different Faraday constants or universal gas constants, or your temperature was more like `"298 K"`.