Question

How do you balance this reaction? `"K"_2"Cr"_2"O"_7(aq) + "H"_2"SO"_4(aq) + "H"_2"S"(aq) -> "Cr"_2("SO"_4)_3(aq) + "H"_2"O"(l) + "S"(s) + "K"_2"SO"_4(aq)`

Answer 1

Here's what I got.

Explanation:

Start by writing the unbalanced chemical equation.

Potassium dichromate, `"K"_2"Cr"_2"O"_7`, will react with hydrosulfuric acid, which is aqueous hydrogen sulfide, `"H"_2"S"`, in acidic medium to precipitate sulfur, `"S"`, and produce aqueous chromium(III) sulfate, `"Cr"_2("SO"_4)_3`, potassium sulfate, `"K"_2"SO"_4`, and water.

`"K"_ 2"Cr"_ 2"O"_ (7(aq)) + "H"_ 2"S"_ ((aq)) + "H"_ 2"SO"_ (4(aq)) -> "Cr"_ 2("SO"_ 4)_ (3(aq)) + "S"_ ((s)) darr + "K"_ 2"SO"_ (4(aq)) + "H"_ 2"O"_ ((l))`

This is a redox reaction in which chromium is being reduced and sulfur is being oxidized.

To make things easier to manage, rewrite this as

`"Cr"_2"O"_7^(2-) + "S"^(2-) -> "Cr"^(3+) + "S"`

The oxidation state of chromium goes from `color(blue)(+6)` in the dichromate anion, `"Cr"_2"O"_7^(2-)`, to `color(blue)(+3)` in the chromium(III) cation, `"Cr"^(3+)`.

• The reduction half-reaction looks like this

`stackrel(color(blue)(+6))("Cr")_ 2 "O"_7^(2-) + 6"e"^(-) -> 2stackrel(color(blue)(+3))("Cr")""^(3+)`

Here each chromium atom gains `3` electrons `(color(blue)(+6) -> color(blue)(+3))`, so two chromium atoms will gain a total of `6` electrons.

Since the reaction takes place in acidic medium, you can balance the oxygen atoms by adding water to the side that needs oxygen and the hydrogen atoms by adding protons, `"H"^(+)`, to the side that needs it.

In this half-reaction, you have `7` atoms of oxygen on the reactants' side, so add `7` water molecules on the product's side

`stackrel(color(blue)(+6))("Cr")_ 2 "O"_7^(2-) + 6"e"^(-) -> 2stackrel(color(blue)(+3))("Cr")""^(3+) + 7"H"_2"O"`

Balance the hydrogen atoms by adding `14` protons on the reactants' side

`14"H"^(+) + stackrel(color(blue)(+6))("Cr")_ 2 "O"_7^(2-) + 6"e"^(-) -> 2stackrel(color(blue)(+3))("Cr")""^(3+) + 7"H"_2"O"`

The oxidation state of sulfur goes from `color(blue)(-2)` in hydrosulfuric acid to `0` in solid sulfur, `"S"`.

• The oxidation half-reaction looks like this

`stackrel(color(blue)(-2))("S")""^(2-) -> stackrel(color(blue)(0))"S" + 2"e"^(-)`

Here each atom of sulfur loses `2` electrons

Now, in any redox reaction the number of electrons lost in the oxidation half-reaction must be equal to the number of electrons gained in the reduction half-reaction.

In your case, you need to multiply the oxidation half-reaction by `color(purple)(3)`, then add the two half-reactions to get

`{ (14"H"^(+) + stackrel(color(blue)(+6))("Cr")_ 2 "O"_7^(2-) + 6"e"^(-) -> 2stackrel(color(blue)(+3))("Cr")""^(3+) + 7"H"_2"O"), (color(white)(aaaaaaaaaaaaaaa)stackrel(color(blue)(-2))("S")""^(2-) -> stackrel(color(blue)(0))"S" + 2"e"^(-)" " " " " " |xxcolor(purple)(3)) :}`
`color(white)(aaaaaaaaaaaaaaaaaaaaaaaaaa)/(color(white)(aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa)`

`14"H"^(+) + "Cr"_ 2"O"_7^(2-) + color(red)(cancel(color(black)(6"e"^(-)))) + color(purple)(3)"S"^(2-) -> 2"Cr"^(3+) + color(red)(cancel(color(black)(6"e"^(-)))) + color(purple)(3)"S" + 7"H"_2"O"`

This is equivalent to

`14"H"^(+) + "Cr"_2"O"_7^(2-) + color(purple)(3)"S"^(2-) -> 2"Cr"^(3+) + color(purple)(3)"S" + 7"H"_2"O"`

Finally, bring in the potassium cations and the sulfate anions to get

`"K"_ 2"Cr"_ 2"O"_7 + color(purple)(3)"H"_2"S" + "H"_2"SO"_4 -> "Cr"_2("SO"_4)_3 + color(purple)(3)"S" + "K"_2"SO"_4 + 7"H"_2"O"`

Notice that you have a total of `4` sulfate anions, `"SO"_4^(2-)`, on the products' side and only `1` on the reactants' side, so multiply sulfuric acid by `4` to get

`"K"_ 2"Cr"_ 2"O"_7 + color(purple)(3)"H"_2"S" + 4"H"_2"SO"_4 -> "Cr"_2("SO"_4)_3 + color(purple)(3)"S" + "K"_2"SO"_4 + 7"H"_2"O"`

Now, you need to have a total of `14` hydrogen atoms on the reactants' side. Check to see if this is the case.

`color(purple)(3)"H"_2"S " color(white)(a)-> color(purple)(3) xx 2 = "6 atoms of H"`

`4"H"_2"SO"_4 -> 4 xx 2 = "8 atoms of H"`

As you can see, you have the number of hydrogen atoms needed for the balanced chemical equation.

Therefore, the balanced chemical equation is

`"K"_ 2"Cr"_ 2"O"_ (7(aq)) + 3"H"_ 2"S"_ ((aq)) + 4"H"_ 2"SO"_ (4(aq)) -> "Cr"_ 2("SO"_ 4)_ (3(aq)) + 3"S"_ ((s)) darr + "K"_ 2"SO"_ (4(aq)) + 7"H"_ 2"O"_ ((l))`

Answer 2

I got

`"K"_2"Cr"_2"O"_7(aq) + 4"H"_2"SO"_4(aq) + 3"H"_2"S"(aq) -> "Cr"_2("SO"_4)_3(aq) + 7"H"_2"O"(l) + 3"S"(s) + "K"_2"SO"_4(aq)`

as well.

---

DISCLAIMER: LONG ANSWER!

Here's an alternative approach to this, using Latimer and Pourbaix diagrams.

Notice how there's `"H"_2"SO"_4`, which is a strong acid. That tells you to balance this reaction in fairly acidic solution.

REDUCTION HALF-REACTION (AND RATIONALE)

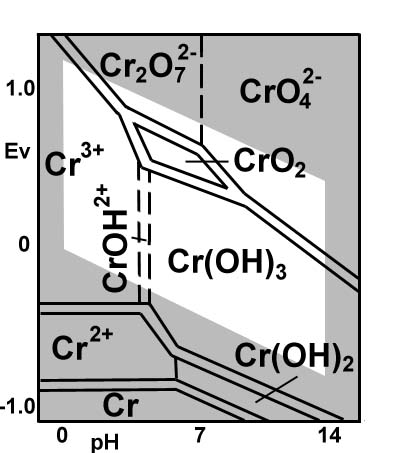
Note this Pourbaix diagram of chromium.

It is a voltage vs. pH diagram, and has many of chromium's preferred states of existence, ordered by oxidation state (more positive at the top, less positive at the bottom).

In acidic pH, we are on the left side of the diagram. You'll find that this diagram has `"Cr"_2"O"_7^(2-)` on it, the dichromate ion, whose chromium's oxidation state is `color(red)(+6)`.

Next, dichromate ion (`"Cr"_2"O"_7^(2-)`) has many oxygens. This makes it a good oxidizing agent.

Also, it is very high up on the Pourbaix diagram, corresponding to a very high oxidation state for chromium.

The highly positive oxidation state of chromium further means that `"Cr"_2"O"_7^(2-)` is a good candidate to be reduced as `stackrel(color(red)(+6))("Cr")_2"O"_7^(2-) -> stackrel(color(red)(+3))("Cr"^(3+))`.

For reduction at constant pH, you move straight downwards on Pourbaix diagrams (applying negative voltage), and that's just the next chromium species you encounter.

We first balance the chromiums to get:

`"Cr"_2"O"_7^(2-)(aq) -> 2"Cr"^(3+)(aq)`

From here, we are balancing this reduction half-reaction in acidic solution. Where I'm from, what I do is:

• add water to balance the oxygens
• add `\mathbf("H"^(+))` to balance the hydrogens
• add electrons to balance the charge

`=> "Cr"_2"O"_7^(2-)(aq) -> 2"Cr"^(3+)(aq) + 7"H"_2"O"(l)`

`=> "Cr"_2"O"_7^(2-)(aq) + 14"H"^(+)(aq) -> 2"Cr"^(3+)(aq) + 7"H"_2"O"(l)`

`=> color(highlight)(stackrel(color(red)(+6))("Cr")_2stackrel(color(red)(-2))("O"_7^(2-))(aq) + 14stackrel(color(red)(+1))("H"^(+))(aq) + 6e^(-) -> 2stackrel(color(red)(+3))("Cr"^(3+))(aq) + 7stackrel(color(red)(+1))("H")_2stackrel(color(red)(-2))("O")(l))`

Alright, now what about that `"H"_2"S"`? Well, it has to be oxidized in a redox reaction, since `"Cr"` has been reduced.

OXIDATION HALF-REACTION (AND RATIONALE)

`"H"_2"S"` has a sulfur with an oxidation state of `-2`. If you take a glance at this Latimer diagram for acidic solutions:

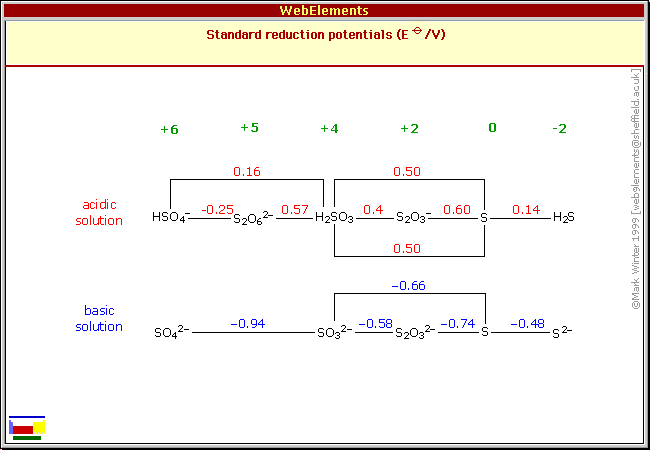
At the top right, you should see that `"H"_2"S"` can get oxidized as `stackrel(color(red)(-2))("S") -> stackrel(color(red)(0))("S")` in one step to the left.

(Granted, that only requires a magnitude of `"0.14 V"`, but not much voltage is required to go from `"Cr"_2"O"_7^(2-)` to `"Cr"^(3+)` at about `3.5` pH, either---easy to accomplish with sulfuric acid. So, we can expect the oxidation to stop there.)

Therefore, the oxidation half-reaction works as follows:

`"H"_2"S"(aq) -> "S"(s)`

There are no oxygens here. So now, we just balance the hydrogens and rebalance the charge.

`=> "H"_2"S"(aq) -> "S"(s) + 2"H"^(+)(aq)`

`=> color(highlight)(stackrel(color(red)(+1))("H")_2stackrel(color(red)(-2))("S")(aq) -> stackrel(color(red)(0))("S")(s) + 2stackrel(color(red)(+1))("H"^(+))(aq) + 2e^(-))`

OVERALL REACTION

Finally, combine these half-reactions back together. Remember that the electrons must cancel out, since they are merely an accounting scheme and are not actually present in solution.

`"Cr"_2"O"_7^(2-)(aq) + 14"H"^(+)(aq) + cancel(6e^(-)) -> 2"Cr"^(3+)(aq) + 7"H"_2"O"(l)`
`3("H"_2"S"(aq) -> "S"(s) + 2"H"^(+)(aq) + cancel(2e^(-)))`
`"-----------------------------------------------"`
`"Cr"_2"O"_7^(2-)(aq) + cancel(14)^(8)"H"^(+)(aq) + "H"_2"S"(aq) -> 2"Cr"^(3+)(aq) + 7"H"_2"O"(l) + "S"(s) + cancel(6"H"^(+)(aq))`

`=> color(green)("Cr"_2"O"_7^(2-)(aq) + 8"H"^(+)(aq) + 3"H"_2"S"(aq) -> 2"Cr"^(3+)(aq) + 7"H"_2"O"(l) + 3"S"(s))`

Normally you'd be done here, but I should add back in the spectator ions to show you that `"H"_2"SO"_4`, `"SO"_4^(2-)`, and `"K"^(+)` are still here.

`=> \mathbf(color(blue)("K"_2"Cr"_2"O"_7(aq) + 4"H"_2"SO"_4(aq) + 3"H"_2"S"(aq) -> "Cr"_2("SO"_4)_3(aq) + 7"H"_2"O"(l) + 3"S"(s) + "K"_2"SO"_4(aq)))`

(Note that I added `"K"_2"SO"_4` last by counting up how many `"SO"_4` are present on each side, since it is made up of both spectator ions, not just one of them.)

---

If you wanted, you could tally up the species to make sure this is balanced.

• `\mathbf(2xx"K")` on each side
• `4 + 3 = 3 + 3 + 1 = \mathbf(7xx"S")` on each side
• `\mathbf(2xx"Cr")` on each side
• `4xx2 + 3xx2 = 7xx2 = \mathbf(14xx"H")` on each isde
• `7+4xx4 = 4xx3 + 7 + 4 = \mathbf(23xx"O")` on each side