Question #efb97
1 Answer
Let the three resistances (resistors)
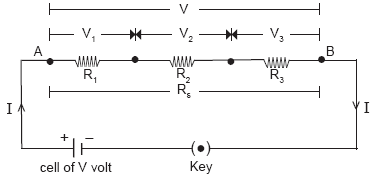
Let
We see that as there is only one path for the current to flow. Therefore, the current through each of the resistors is the same.
By Ohm’s law, the potential differences across the three resistors is,
Also, the voltage drops across the resistors must add up to the total voltage supplied by the battery, we have
As Ohm's Law must also be satisfied for the complete circuit, we have
Comparing (1) and (2) we have
In general, the equivalent resistance of resistors when connected in series is the sum of all resistances.
