Question #d0cfc
1 Answer
Here's how you could do it:
Explanation:
It seems you need to produce a calibration curve for the distance measured against the wavelength of the emission line using Excel.
I got this from your data:
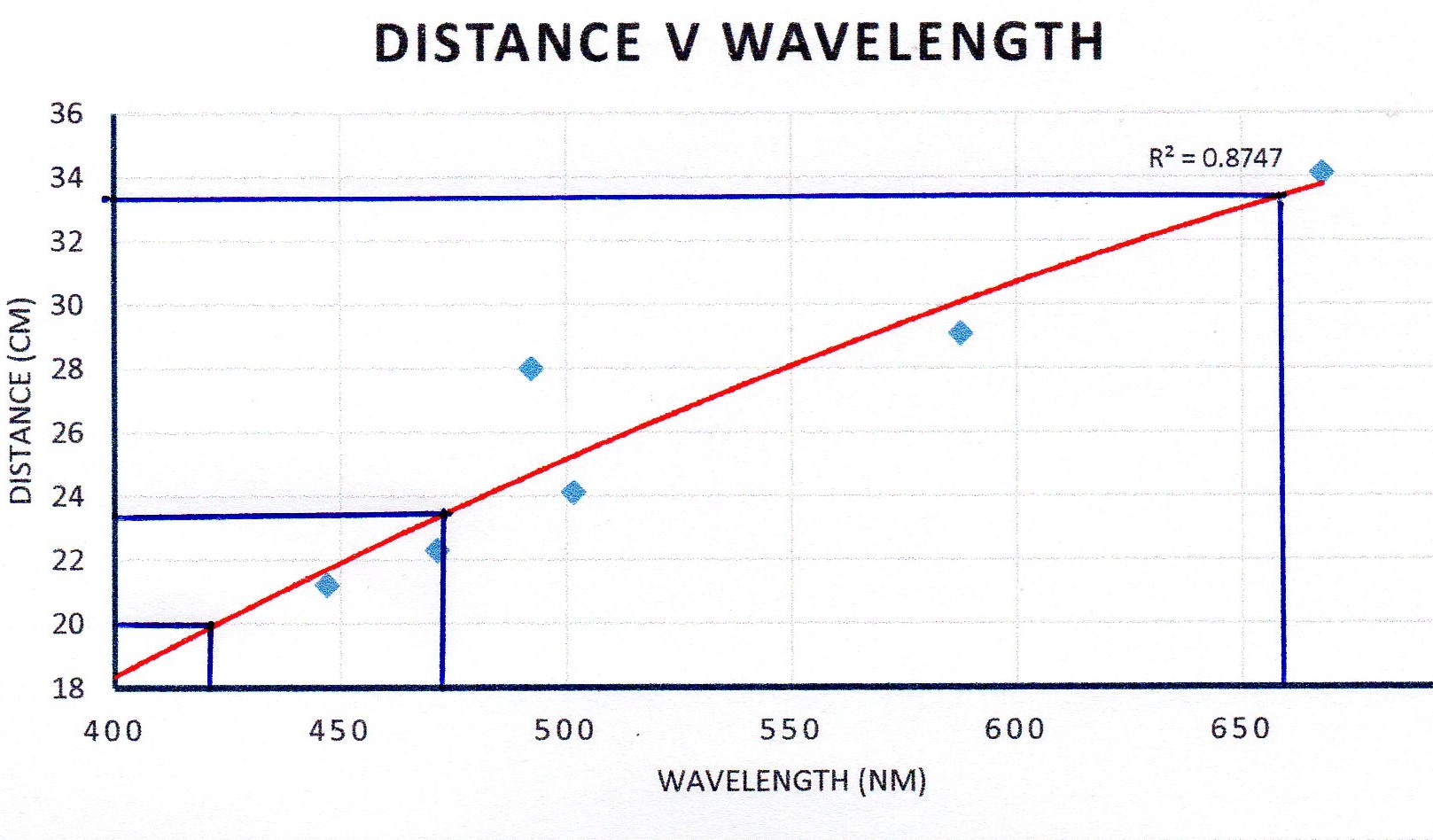
I assumed cm but I guess it could be mm - you should put this on your table.
Point 28 is an outlier - you should repeat this if you can.
I then used the 3 lines from the hydrogen lamp to read off the values of the wavelength.
I can't read your worksheet too well, it seems you are asked for a linear plot.
To do this enter your data in a table and make a scatter chart. Click on a data point and "add trend line". You can select "linear" and it will give you the line of best fit through the points.
You can select "display
The
This means the correlation coefficient
I have manually read the wavelengths off the chart, though you could use the equation given.
So for red:
This is an experimental value. You are asked to compare this with the calculated value using the Rydberg Equation:
The Balmer Series, which you are dealing with, involves transitions down to the

The red emission line will be the lowest in energy so will have the longest wavelength corresponding to
Putting this into the Rydberg Expression:
(You made a mistake in your annotation and wrote
So we have:
Experimental:
Theoretical:
That's reasonably good. You can work out the difference as a percentage as asked for in your error calculation.
Then work out

