What are the strengths and weaknesses of the Fibonacci sequence?
1 Answer
A few thoughts...
Explanation:
The Fibonacci sequence is the Fibonacci sequence. In what sense would we consider it to have strengths and weaknesses?
-
As a teaching example?
-
As an example of principles required when working with sequences in general?
-
As an example of a sequence most naturally defined by a recursive rule?
-
For its mathematical significance?
Let's take a look:
The normal recursive definition of the Fibonacci sequence can be written like this:
#{(F_0 = 0), (F_1 = 1), (F_(n+2) = F_(n+1) + F_(n)" "(n >= 0)) :}#
#0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,...#
The ratio
Due to the way it's defined, the successive approximations
#[1;bar(1)] = 1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+...)))))))#
This is the slowest converging continued fraction possible.
In one sense it's very easy to work with, but the slow convergence is not so nice.
A rectangle with sides in golden ratio has the property that when the largest possible square is removed from one end, the remaining rectangle is in golden ratio. Conversely, we can combine squares with sides from the Fibonacci sequence to approximate a golden rectangle...
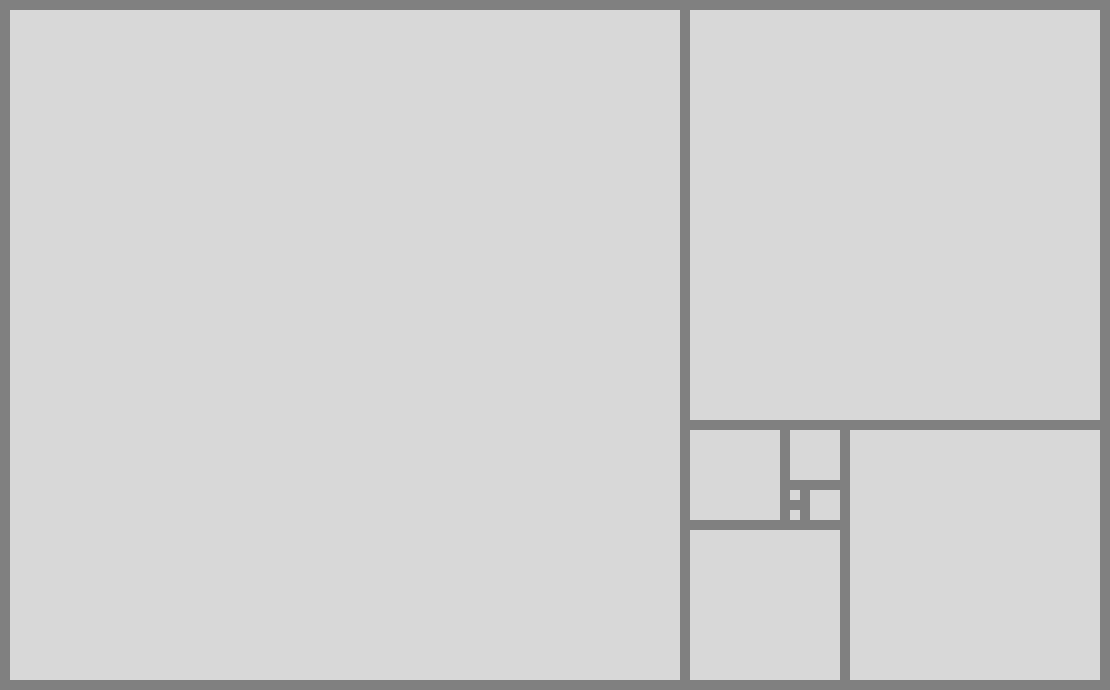
Three rectangles in golden ratio, placed symmetrically at right angles to one another, cutting through the middle of one other, have corners at the vertices of a regular icosahedron.
It is fairly straightforward to take the recursive definition of
#F_n = (varphi^n - (-varphi)^(-n))/sqrt(5)#
This derivation can be used as a useful example of how to construct such direct formulas from similar recursive definitions, or alternatively as an example proof by induction.
Conclusion
The Fibonacci sequence is a beautiful, simple sequence with many interesting properties. It makes a very good and seriously useful teaching example.

