Question #24349
1 Answer
Explanation:
Here's my interpretation of the problem
The specific volume of a cylindrical virus particle is equal to
#6.02 * 10^(-2)"cm"^3"g"^(-1)# . The radius of the particle is equal to#7Å# and its height is equal to#10Å# . What is the molecular mass of the virus?
If this is indeed what your problem looks like, then your starting point here will be the specific volume,
The specific volume of a given substance is defined as the ratio between the volume of the substance and the mass it occupies. In your case, the virus is said to have a specific volume of
#v = 6.02 * 10^(-2)"cm"^3"g"^(-1)#
This means that for every gram of virus particles you get a volume of
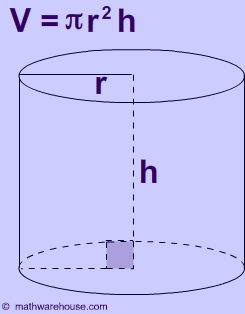
Now, the virus is said to be shaped like a cylinder.
The volume of a cylinder is given by the equation
#color(blue)(|bar(ul(color(white)(a/a)V = pi * r^2 * hcolor(white)(a/a)|)))#
In your case, the radius of the cylinder,
#r = 7Å = 7 * 10^(-10)"m"#
The height of the cylinder is said to be
#h = 10Å = 10 * 10^(-10)"m"#
Since the specific volume of the virus is expressed in cubic centimeters per gram, convert the radius and height of the cylinder to centimeters
#7 * 10^(-10) color(red)(cancel(color(black)("m"))) * (10^2"cm")/(1color(red)(cancel(color(black)("m")))) = 7 * 10^(-8)"cm"#
and
#10 * 10^(-10)color(red)(cancel(color(black)("m"))) * (10^2"cm")/(1color(red)(cancel(color(black)("m")))) = 10^(-7)"cm"#
The volume of one virus particle will this be
#V = pi * (7 * 10^(-8)"cm")^2 * 10^(-7)"cm"#
#V = 1.54 * 10^(-21)"cm"^3#
Use the specific volume of the virus to calculate the mass of one particle
#1.54 * 10^(-21) color(red)(cancel(color(black)("cm"^3))) * "1 g"/(6.02 * 10^(-2)color(red)(cancel(color(black)("cm"^3)))) = 2.56 * 10^(-20)"g"#
In order to find the molecular mass of the virus, you need to find the mass of one mole of virus particles.
As you know, Avogadro's number gives you the number of particles present in one mole
#color(blue)(|bar(ul(color(white)(a/a)"1 mole" = 6.022 * 10^(23)"particles" color(white)(a/a)|))) -># Avogadro's number
Use the mass of one particle to find the mass of one mole of particles
#2.56 * 10^(-20)"g"/color(red)(cancel(color(black)("particle"))) * (6.022 * 10^(23)color(red)(cancel(color(black)("particles"))))/"1 mole" = color(green)(|bar(ul(color(white)(a/a)color(black)(1.5 * 10^(4)"g mol"^(-1))color(white)(a/a)|)))#
I'll leave the answer rounded to two sig figs, but keep in mind that the values given to your for the radius and height of the cylinder justify only one sig fig.