Question

Is it true that `cos^(-1) x = 1/cos x` ?

Answer 1

False due to a clash of conventions.

Explanation:

If `n > 1` is a positive integer, then:

`cos^n x = (cos x)^n`

This is a convenience of notation, to avoid having to use parentheses to distinguish, for example:

`(cos x)^2` and `cos (x^2)`

By convention we can write:

`cos^2 x` and `cos x^2`

respectively, without ambiguity.

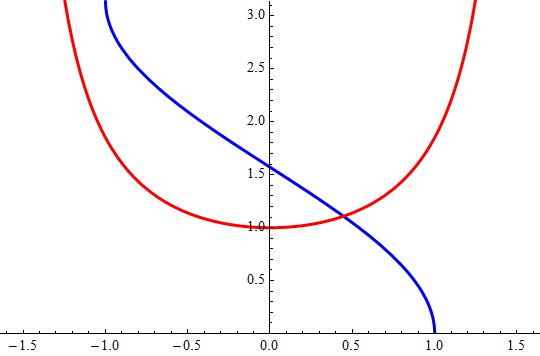
However, in the case of `-1`, we have a clash of notation. If `f(x)` is a function, then `f^(-1)(x)` is the inverse function. So we denote the inverse of the function `cos x` by `cos^(-1) x`.

graph{y=arccos x [-5.13, 4.87, -1.04, 3.96]}

This is not to be confused with the reciprocal `(cos x)^(-1) = 1/(cos x)`.

graph{1/cos x [-10.3, 9.7, -4.9, 5.1]}

Since there is no other convenient notation for the inverse function (apart from the ungainly name `arccos`), we give it priority when it comes to the expression `cos^(-1) x`.

Sorry.

Answer 2

Depends if you consider it as an equation or as an identity.

Explanation:

This affirmation has sense only as an equation.
Iteratively you can find a solution such as

`arccos(0.446048) = 1/cos(0.446048)`

Attached a plot showing `arccos(x)` in blue and `1/cos(x)` in red.