Question

Question #e734d

Answer 1

The required Normals are at the points `(0, -1), (2,1)` They coincide and the equation is `y = x-1`

Explanation:

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is `−1`).

So, if we the gradient of the normal, `m_N=1` then the gradient of the tangent, `m_T=-1`

We have:

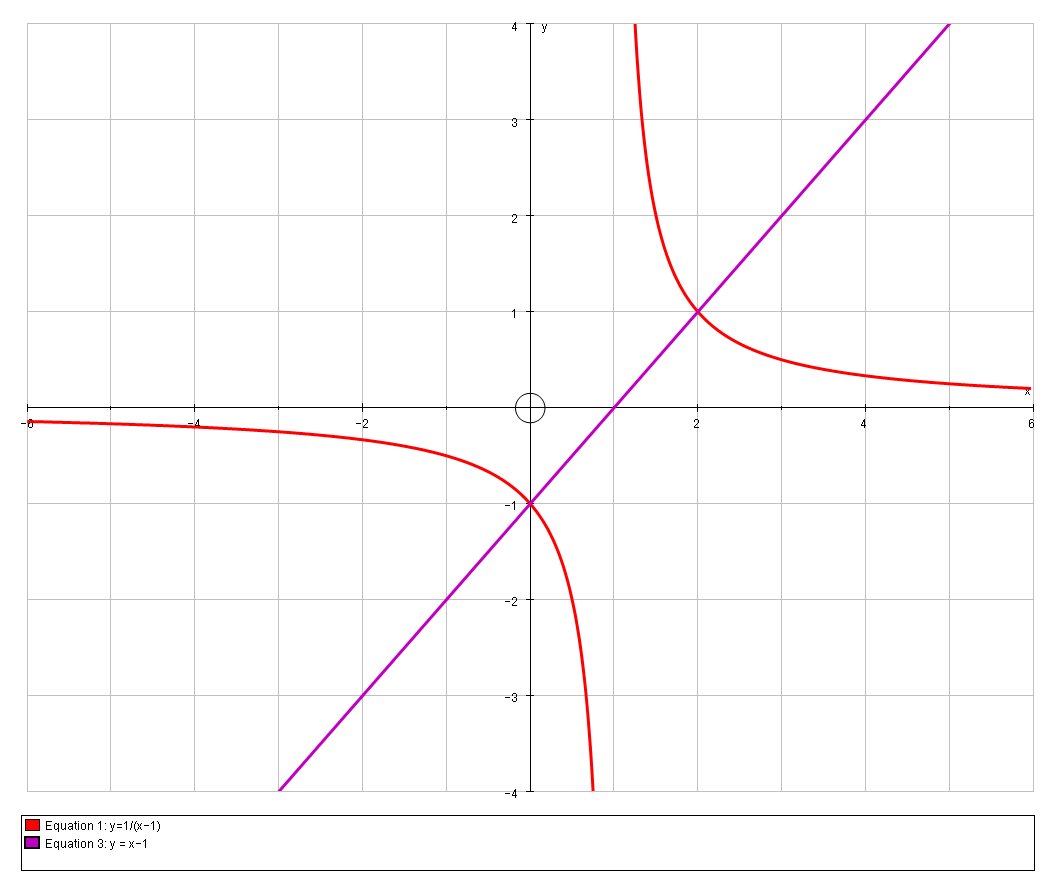
`y = 1/(x-1)`

Differentiating wrt `x` we get

`dy/dx = -1/(x-1)^2`

So if the slope is to be `m_T=-1`, then:

`dy/dx = -1 => -1/(x-1)^2 = -1`
`:. (x-1)^2 =1`
`:. x^2-2x+1 = 1`
`:. x^2-2x = 0`
`:. x(x-2) = 0 => x = 0,2`

This leads to two possible coordinates:

`(0, -1), (2,1)`

So using the point/slope form `y-y_1=m(x-x_1)` the normal equations we seek are;

At `(0,-1)` the equation is:

`y - (-1) = (1)(x-0 )`
`:. y + 1 = x`
`:. y = x-1`

At `(2,1)` the equation is:

`y - 1 = (1)(x-2 )`
`:. y - 1 = x-2`
`:. y = x-1`

So the normals coincide: