Given a list of values #{x_k,y_k}, k=1,2,cdots,n#
a line can be adjusted such that the accumulated deviation error is minimum.
Let the line be given by
#y = a x + b#
then the error at point #x_k# is #e_k = y_k - (a x_k + b)#
The accumulated quadratic error will be given by
#E(a,b) = sum_(k=1)^n e_k^2 =sum_(k=1)^n( y_k - (a x_k + b))^2#
#E(a,b)# have a minimum for #a_0,b_0# such that
#(partial E)/(partial a)(a_0,b_0) = 0-> b_0 sum x_k+a_0 sumx_k^2=sum x_ky_k#
#(partial E)/(partial b)(a_0,b_0) = 0 -> n b_0 + a_0 sum x_k =sum y_k #
solving for #a_0,b_0#
#a_0 = ( (sum x_k)( sum y_k)-n sum x_ky_k)/((sum x_k)^2-nsum x_k^2)#
#b_0 = ((sum x_k)(sum x_ky_k)-(sum x_k^2)(sum y_k))/((sum x_k)^2-nsum x_k^2#
appliying it to the table
#{{10,15}, {10,25}, {15,17}, {17,20}, {25,11.5}, {30,11},{35,5},{35,10}}#
we obtain:
#a_0 = -0.489421, b_0 = 25.3113#
so the adjusting line is
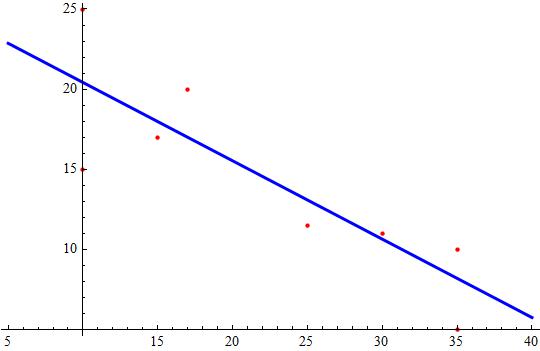
#y = -0.489421 x + 25.3113#
Attached a plot