Question #aa655
1 Answer
Here's how you can do that.
Explanation:
The units given to use are expressed using metric prefixes, which as you know are based on the powers of
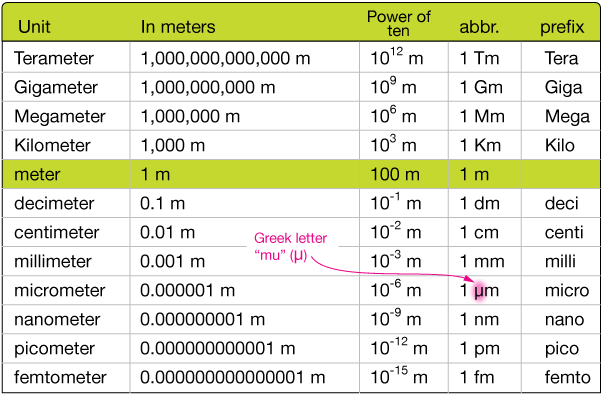
#color(blue)(ul(color(black)("going from"color(white)(a)mu"g to g or vice versa"))#
The prefix micro is used to denote a fraction of a given unit. In this case, a microgram is simply a fraction of a gram, i.e. you can get from micrograms to grams by dividing by a number.
More specifically, a microgram is the
#color(purple)(bar(ul(|color(white)(a/a)color(black)("1 g" = 10^6mu"g")color(white)(a/a)|)))#
This means that
- you get from micrograms to grams by dividing by
#10^6# - you get from grams to micrograms by multiplying by
#10^6#
So micro simply means that you must divide by
#color(blue)(ul(color(black)("going from kL to cL or vice versa"))#
Here the prefix kilo is used to denote a multiple of a base unit and the prefix centi is used to denote a fraction of a unit.
More specifically, you get from kiloliters to liters by multiplying by
#color(purple)(bar(ul(|color(white)(a/a)color(black)("1 kL" = 10^3"L")color(white)(a/a)|)))" "# and#" "color(purple)(bar(ul(|color(white)(a/a)color(black)("1 L" = 10^2"cL")color(white)(a/a)|)))#
This means that you can use the liter to find a direct conversion factor between kiloliters and centiliters
#1 color(red)(cancel(color(black)("kL"))) * (10^3color(red)(cancel(color(black)("L"))))/(1color(red)(cancel(color(black)("kL")))) * (10^2"cL")/(1color(red)(cancel(color(black)("L")))) = 10^5"cL"#
This means that
- you get from centiliters to kiloliters by dividing by
#10^5# - you get from kiloliters to centiliters by multiplying by
#10^5#
#color(blue)(ul(color(black)("going from nm to mm or vice versa"))#
This time, you're dealing with two prefixes that are used to denote fractions of a base unit.
You can go from millimeters to meters by dividing by
#color(purple)(bar(ul(|color(white)(a/a)color(black)("1 m" = 10^3"mm")color(white)(a/a)|)))" "# and#" "color(purple)(bar(ul(|color(white)(a/a)color(black)("1 m" = 10^9"nm")color(white)(a/a)|)))#
A direct conversion factor between millimeters and nanometers would look like this
#1 color(red)(cancel(color(black)("mm"))) * (1 color(red)(cancel(color(black)("m"))))/(10^3color(red)(cancel(color(black)("mm")))) * (10^9"nm")/(1color(red)(cancel(color(black)("m")))) = 10^(6)"nm"#
This means that
- you get from nanometers to millimeters by dividing by
#10^6# - you get from millimeters to nanometers by multiplying by
#10^6#

