Based on comments from the other answer, the intended function was #"floor"(x/2)#, that is, the function on #RR# whose output is the greatest integer less than or equal to the input. Let #f(x) = "floor"(x)#. Then a graph of #f(x)# looks like this:
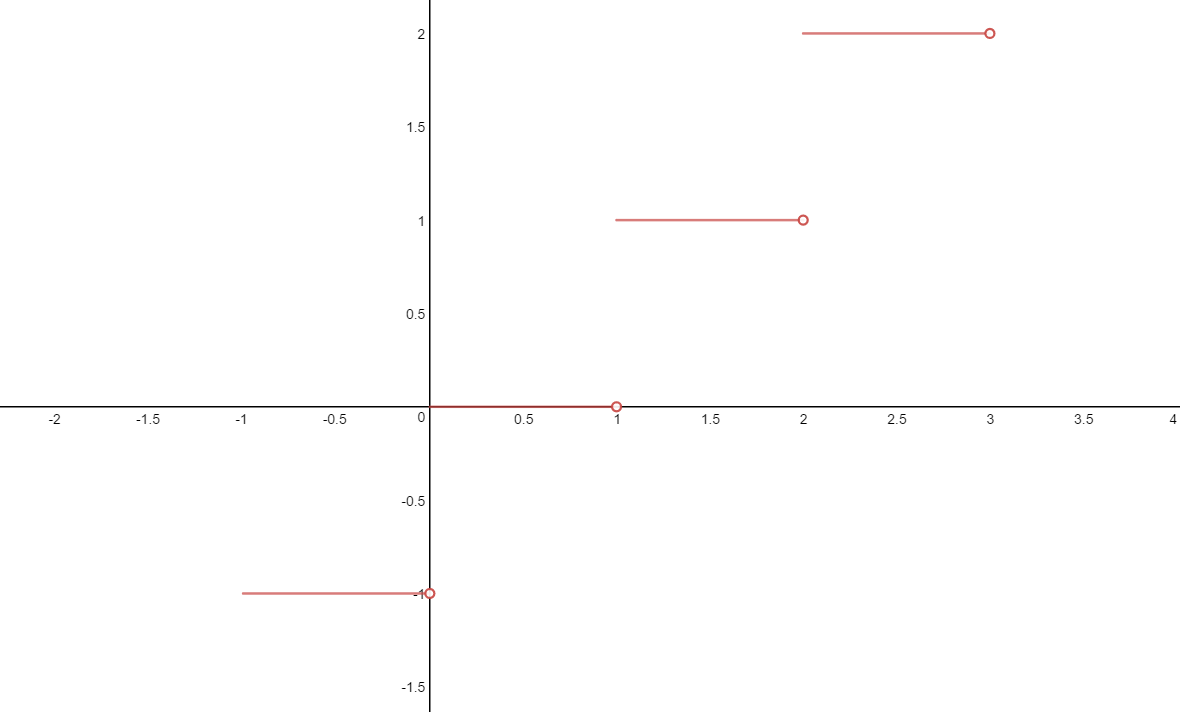
Notice that points of discontinuity occur every time we approach an integral value. When we reach that value, we jump from the lesser integer less than that value to that value (notice these are jump discontinuities) If we instead apply #f# to #x/2#, then those integral values will occur only half as often, at #x in {...-2, 0, 2, 4, ...}#. This will cause the line segments to extend:
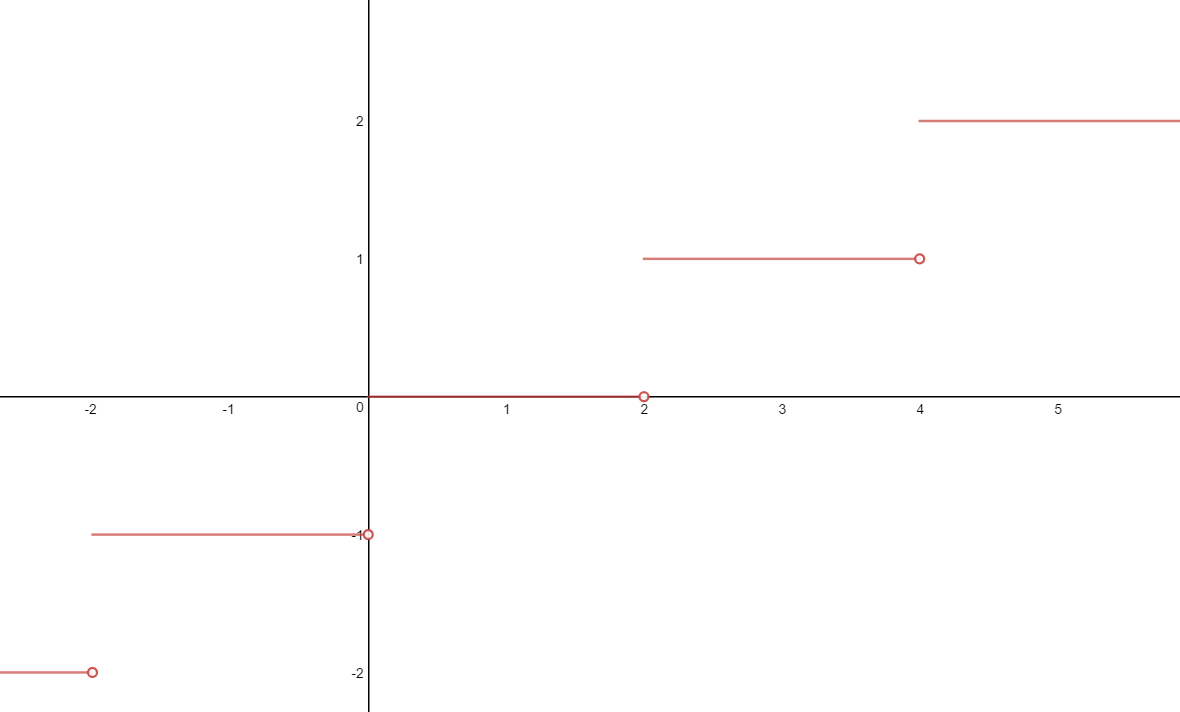
So the points of discontinuity occur for #f(x/2)# at each even integer.
Now, #f(x/2)# is clearly continuous at every #x!in{...-2,0,2,4,...}#, so we will now examine whether it is left or right continuous at those points.
Notice that if we approach an even value of #x# from the right, we are traveling along a constant line whose value matches #f(x/2)#. For example, #lim_(x->2^+)f(x/2) = lim_(x->2^+)1 = 1#, as #f(x/2)# matches the constant function #1# on the right side of #x=2#. In fact, this is the case at every even integer, meaning we have #lim_(x->x_0^+)f(x/2) = f(x_0/2)# for all #x in RR#. Thus, #f(x/2)# is right-continuous.
If we approach from the left, however, we get a different result. Let's look at #x=2# again.
#lim_(x->2^-)f(x/2) = lim_(x->2^-)0 = 0#, as #f(x/2)# matches the constant function #0# on the left side of #x=2#. As #lim_(x->2^-)!=f(2/2)#, this means #f(x/2)# is not left-continuous at #x=2#. Indeed, this is the case at every even integer. So, taken together, we get, using the notation #2ZZ# to represent the even integers:
#f(x)# has jump discontinuities at #x in 2ZZ#
#f(x)# is right-continuous on #RR#
#f(x)# is left-continuous on #RR-2ZZ#



