Question #67cea
1 Answer
Jul 14, 2017
Here's what I get.
Explanation:
(a) Exponential decay model
The rate law for a first-order reaction is
where
Now,
(I had to write the half-life as
In this problem,
So, your exponential expression is
(b) Graph
I plotted the graph in Excel:
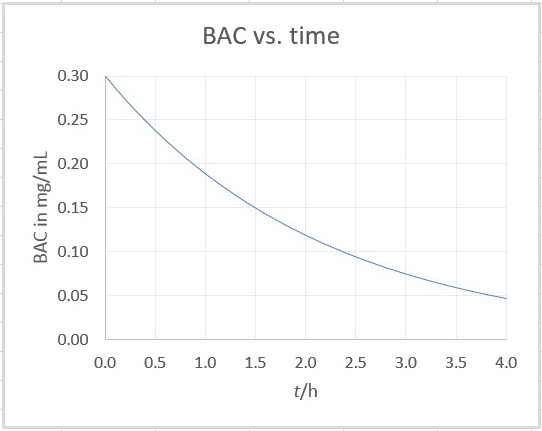
It looks like BAC = 0.075 mg/mol at 3.0 h.
I would guess that BAC = 0.08 mg/mL at 2.9 h.
You can drive home at about 02:55.

