Question

Question #fb7f1

Answer 1

`"130 kg"`

Explanation:

The idea here is that you can treat the lake as a cylinder and use the given diameter and depth to find its approximate volume.

As you can see, the diameter is given in miles and the average depth in meters, so the first thing to do here is to convert the diameter to meters.

To do that, go from miles to kilometers first, then from kilometers to meters

`10 color(red)(cancel(color(black)("mi"))) * (1.61color(red)(cancel(color(black)("km"))))/(1color(red)(cancel(color(black)("mi")))) * (10^3"m")/(1color(red)(cancel(color(black)("km")))) = "16100 m"`

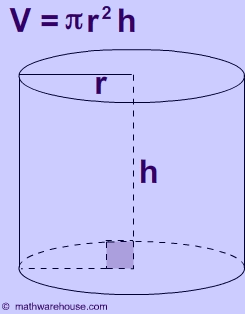
Now, the volume of a cylinder can be calculated using the equation

Here the radius of the lake is equal to half of the diameter, so

`r = "16100 m"/2 = "8050 m"`

The height of the cylinder is actually the depth of the lake, so

`V = pi * ("8050 m")^2 * "50 m"`

`V ~~ 1.02 * 10^10"m"^3`

Notice that the concentration of mercury is given in micrograms per liter, `mu"g L"^(-1)`, so make sure to convert the volume from cubic meters to liters

`1.02 * 10^(10) color(red)(cancel(color(black)("m"^3))) * (10^3"L")/(1color(red)(cancel(color(black)("m"^3)))) = 1.02 * 10^(13)"L"`

This means that the concentration of mercury in micrograms will be

`1.02 * 10^(13)color(red)(cancel(color(black)("L"))) * (0.0125color(white)(a)mu"L")/(1color(red)(cancel(color(black)("L")))) = 1.275 * 10^(11)mu"g"`

To convert this to kilograms, go to grams first

`1.275 * 10^(11)color(red)(cancel(color(black)(mu"g"))) * (1color(red)(cancel(color(black)("g"))))/(10^6color(red)(cancel(color(black)(mu"g")))) * "1 kg"/(10^3color(red)(cancel(color(black)("g")))) = color(green)(bar(ul(|color(white)(a/a)color(black)("130 kg")color(white)(a/a)|)))`

I'll leave the answer rounded to two sig figs.