Question #a6088
1 Answer
(a)
(b) Steps as below.
Explanation:
Imagine the following as shown in the figure below:
At the moment when the package is released it is traveling equal to the speed of the plane.
∴ Use the following.
Projectile (Package released by the pilot) has initial velocity of
Taking origin of coordinate system at the point of release of packet with positive directions as shown in the figure.
The package has velocity whose
Treat the component velocities of the package separately.
As we assume air friction is negligible there is no change of velocity in the
Acceleration due to gravity is
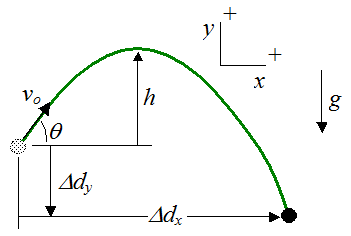
(a). To calculate time of flight
This quadratic equation can be solved by using the formula for
I calculated its roots using the inbuilt graphic utility. We plot this quadratic equation and find out value of

(b). To Calculate Vertical component of velocity as the package hits earth we use the kinematic equation
Inserting given values we get
Resultant of this calculated velocity and Horizontal component of velocity
