What are the periodic trends for atomic radii, ionization energy, and electron affinity?
2 Answers
They will all increase (generally) with increasing atomic number.
Explanation:
Generally, the atomic radius increases with element size (atomic number). Ionization energy and electron affinity also increase with increasing atomic number, but primarily along the same row (left to right) of elements in the Periodic Table.
Of these, atomic radius is the most predictable, and ionization energy and electron affinity trends follow (at least in part) from such trends.
ATOMIC RADII
In general, the atomic radius (except for many transition metals) has a pattern where it decreases from the bottom-left to the top-right of the periodic table.
This is because:
-
Effective nuclear charge increases from left to right.
As we go across the periodic table from left to right, protons are more massive than electrons, so adding one proton and one electron to obtain a new atom means that#bb(Z_("eff")uarr)# . Higher#Z_"eff"# means smaller radius. -
A new quantum level corresponds to the valence shell on a new row (below).
This new quantum level is farther out, and therefore, the radius increases as we go downwards on the periodic table.
Note that it means you cannot, say, compare
IONIZATION ENERGIES
As I said, the ionization energies follow somewhat from atomic radius. The smaller the atomic radius, the more closely the electrons are held by the nucleus, and thus the higher the ionization energy.
So, in general, ionization energy increases from the bottom-left to the upper-right of the periodic table.
There are, however, some exceptions to this general rule, as you can see in the diagram below:
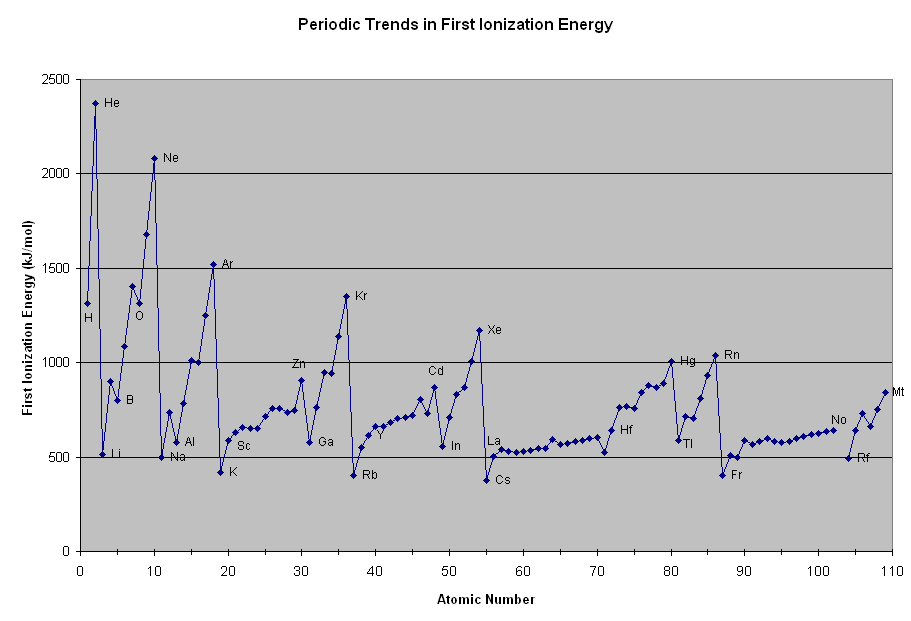
-
Elements on a new row have their final electron start on a new quantum level, so naturally its ionization energy drops a bunch.
-
Elements in the same row that start to fill a new subshell (a new
#bb(l)# ) have a drop in ionization energy downwards.
The new subshell is higher in energy (less core-like). Therefore, the first ionization energy (#"IE"_1# ) for, say,#"B"# , is lower than for#"Be"# , because the#2p# orbitals are higher in energy than the#2s# , and so,#"B"# can be more easily ionized than#"Be"# . -
For elements with electrons in a subshell of
#l >= 1# , once electron pairing starts occurring, the paired electron is easier to remove than an unpaired electron.
Electron pairing causes electron repulsion between like-charges which means that the ionization energy required to remove the first electron (#"IE"_1# ) is smaller. For instance, it is smaller for#"O"# than for#"N"# , since the fourth#2p# electron on#"O"# is paired but the#2p# electrons on#"N"# are not.
ELECTRON AFFINITY
Electron affinity is not particularly patterned or necessarily predictable. In general, smaller atomic radius
So, in general, electron affinity increases from the bottom-left to the top-right of the periodic table.
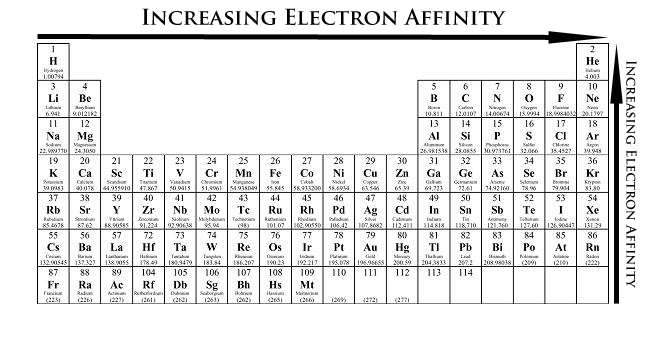
However, as I mentioned, there are some exceptions. See if you can notice such exceptions:



