We can figure out the index of refraction of the sapphire by using the following equation
#color(white)(aaaaaaaaaaaaaaaaaaa)color(magenta)(n = c/v#
Where
#n = "index of refraction"#
#c = "speed of light in a vacuum" (3*10^8m/s)#
#v = "speed of light traveling in medium" (m/s)#
#color(white)(aaaaaaaaa)n = c/v->n = (3*10^8cancel(m/s))/(1.71*10^8cancel(m/s))->n=1.75#
#"Air"# has a refractive index of #1#
#color(white)(aaaaaaaaa)n = c/v->n = (3*10^8cancel(m/s))/(3*10^8cancel(m/s))->n=1.00#
Since the #"speed of light in a vacuum"# is constant, if #"v"# increases, then #"n"# decreases (inverse relationship).
When light travels from 1 transparent medium to another transparent medium, some of the light reflects and some refracts. Depending on the type of medium it is, the refracted ray could bend toward the normal or away from the normal.
#--------------------#
When light travels from a medium #color(red)("where its speed is higher than the medium it enters")#, the refracted ray will bend toward the #"Normal"# and the #"angle of refraction"# #(theta_(r))# will be smaller than the #"angle of incidence"# #(theta_(i))#
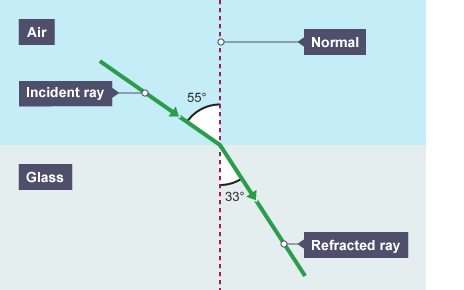
#--------------------#
When light travels from a medium #color(blue)("where its speed is lower than the medium it enters")#, the refracted ray will bend away from the #"Normal"# and the #"angle of refraction"# #(theta_(r))# will be bigger than the #"angle of incidence"# #(theta_(i))#.
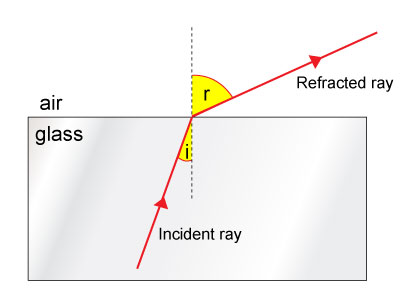
#--------------------#
Now #"total internal reflection"# is something that results from light rays exiting a medium with a higher index of refraction(i.e. sapphire) to a medium with a lower index of refraction (i.e. air).
#color(white)(aaaaaaa)#
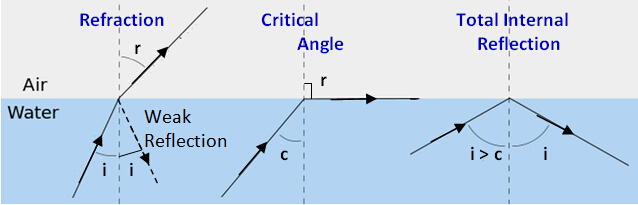
#color(white)(aaaaaaa)#
If we keep increasing the incident angle, the refracted angle just keeps getting bigger. Once the incident angle gets increased to a certain point (critical angle), the refracted angle bends away from the normal so much that the angle formed becomes #90^(@)#. Here, the light rays traveling in this medium will travel parallel to the boundary of the two medium.
Here, we can apply Snell's Law to find our critical angle
#color(white)(aaaaaaaaaaaa)color(magenta)(n_1sin(theta_(c)) = n_2sin(90^(@)) color(white)(aaaa) n_1>n_2#
Where
#n_1 = "index of refraction of medium 1"#
#sin(theta_(c)) = "critical angle"#
#n_2 = "index of refraction of medium 2"#
#sin(90^(@)) = "angle of refraction"#
Rearrange, plugin and solve
#n_1sin(theta_(c)) = n_2sin(90^(@))#
#sin(theta_(c)) = (n_2)/(n_1)#
#(theta_(c)) = sin^(-1)[(n_2)/(n_1)]#
#(theta_(c)) = 34.85^(@)#
Any angle greater than #34.85^(@)# and total internal reflection will occur and all light rays will reflect back into the original medium.




