Question #3b185
1 Answer
Nov 17, 2016
See below.
Explanation:
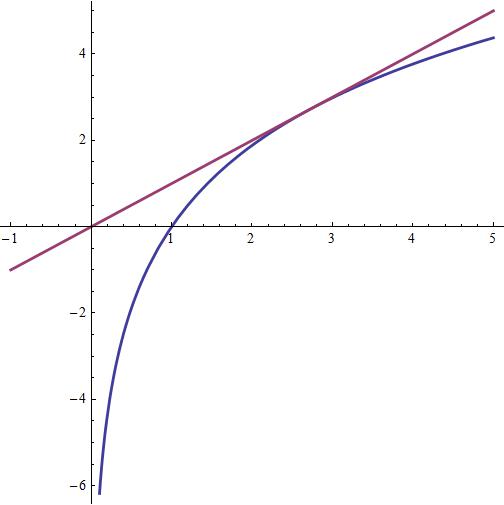
Calling
or at
At this point we have
To qualify this stationary point we compute
The conclusion is:
Note that for
Attached a plot with