Question #e5c2c
2 Answers
Explanation:
If
Explanation:
Suppose
#=d/dx(G(x^2)-G(1))#
#=d/dxG(x^2)-d/dxG(1)#
#=2xG'(x^2)#
#=2xe^(-sin(x^2))#
Then, as
Because
This is the graph of
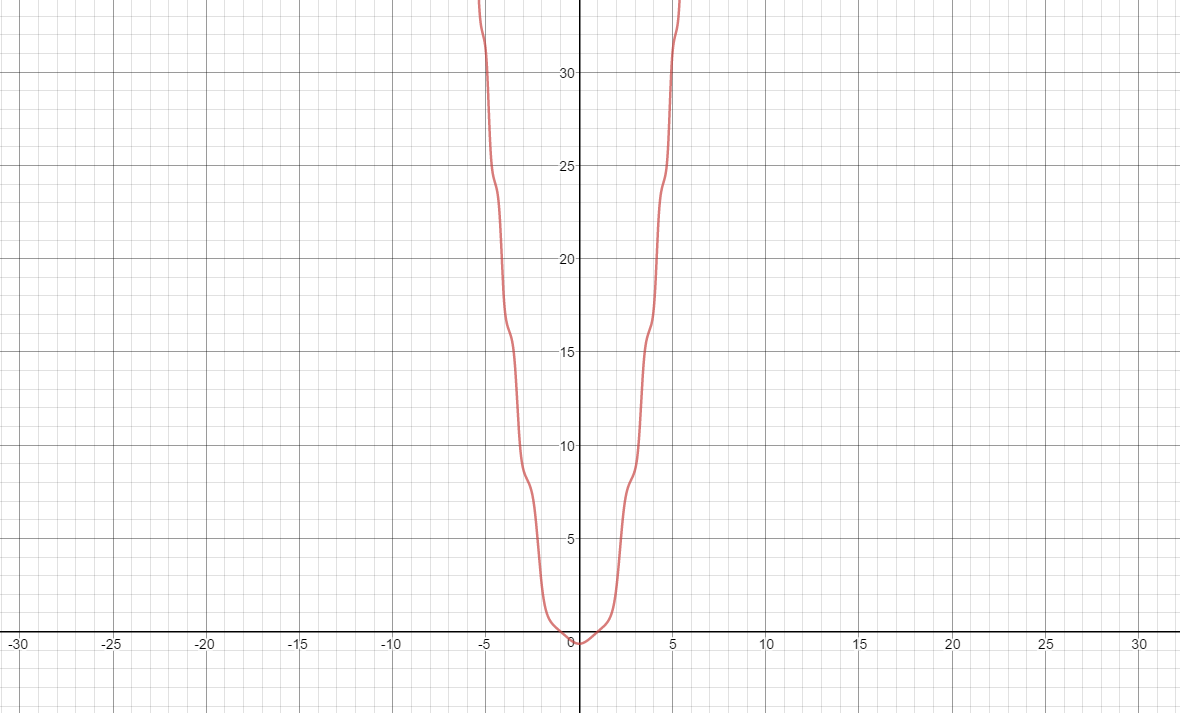
If
Suppose
#=d/dx(G(x^2)-G(1))#
#=d/dxG(x^2)-d/dxG(1)#
#=2xG'(x^2)#
#=2xe^(-sin(x^2))#
Then, as
Because
This is the graph of
