Question #295d0

Question

2017 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-20T17:44:30

#sf(A).#

#sf(DeltaH^@=-217.3color(white)(x)"kJ/mol")#

#sf(B).#

#sf(262.2color(white)(x)kJ)# released.

#sf(A.)#

To do this type of question you need to construct a Hess Cycle.

Hess' Law states that the overall enthalpy change of a chemical reaction is independent of the route taken.

All the substances are made from the same elements so the elements can go on the bottom.

Then construct the cycle:

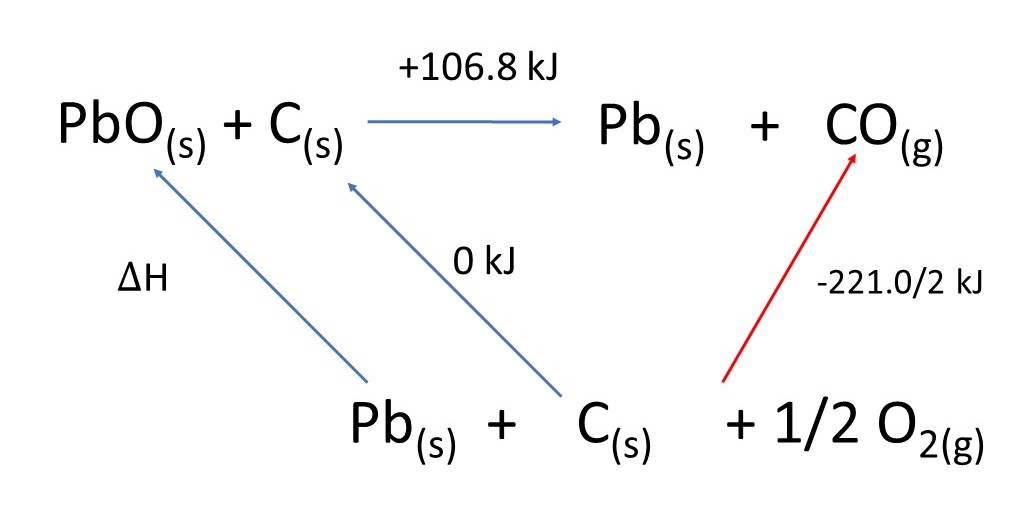
MFDocs

Note that I have divided the enthalpy of formation of #sf(CO)# by 2 since the value given refers to formation of 2 moles.

Also note that the enthalpy formation of the element carbon is zero.

Hess' Law tells us that the enthalpy change of the #sf(color(blue)(blue))# route is equal to the enthalpy change of the #sf(color(red)(red))# route.

This is because the arrows start and finish in the same place.

Applying the law #sf(rArr)#

#sf(DeltaH+0+106.8=-221.0/2)#

#:.##sf(DeltaH=-110.5-106.8=-217.3color(white)(x)kJ)#

This refers to #sf(Pb_((s))+1/2O_(2(g))rarrPbO_((s)))#

#sf(B).#

The #sf(A_r)# of Pb is 207.2

So 1 mole of Pb weighs 207.2 g.

From the equation we can say:

#sf(207.2color(white)(x)grarr-217.3color(white)(x)kJ)#

#:.##sf(1color(white)(x)grarr-217.3/207.2color(white)(x)kJ)#

#:.##sf(250.0color(white)(x)grarr-217.3/(207.2)xx250.0=-262.2color(white)(x)kJ)#

The minus sign tells us that #sf(262.2color(white)(x)kJ)# is released.