If light of frequency #6.90 xx 10^14 "s"^(-1)# is emitted when an electron in hydrogen atom relaxes from #n_1 = 5#, what is #n_2#?
1 Answer
Explanation:
All you have to do here is use the Rydberg equation for hydrogen, which looks like this
#color(blue)(ul(color(black)(1/(lamda) = R * (1/n_2^2 - 1/n_1^2))))#
Here
#lamda# is the wavelength of the emitted photon#R# is the Rydberg constant, equal to#~~1.097 * 10^(7)"m"^(-1)# #n_1# is the principal quantum number that describes the orbital from which the transition is made#n_2# is the principal quantum number that describes the orbital to which the transition is made
Now, notice that the problem provides you with the frequency of the emitted photon, so make sure that you convert it to wavelength by using the equation
#color(blue)(ul(color(black)(lamda * nu = c)))#
Here
#nu# is the frequency of the photon#c# is the speed of light in a vacuum, usually given as#3 * 10^8"m s"^(-1)#
In your case, you will have
#lamda = c/(nu)#
#lamda = (3 * 10^8"m" color(red)(cancel(color(black)("s"^(-1)))))/(6.90 * 10^(14)color(red)(cancel(color(black)("s"^(-1))))) = 4.348 * 10^(-7)"m"#
Rearrange the Rydberg equation to solve for
#1/(lamda) = R * (1/n_2^2 - 1/n_1^2)#
#1/(lamda) * 1/R = (n_1^2 - n_2^2)/(n_1^2 * n_2^2)#
This is equivalent to
#n_1^2 * n_2^2 = lamda * R * n_1^2 - lamda * R * n_2^2#
and so
#n_1^2 * n_2^2 + lamda * R * n_2^2 = lamda * R * n_1^2#
#n_2^2 * (n_1^2 + lamda * R) = lamda * R * n_1^2#
#n_2^2 = (lamda * R * n_1^2)/(n_1^2 + lamda * R)#
Finally,
#n_2 = sqrt( (lamda * R * n_1^2)/(n_1^2 + lamda * R)#
You know that
#n_2 = sqrt( (4.348 * color(blue)(cancel(color(black)(10^(-7)))) color(red)(cancel(color(black)("m"))) * 1.097 * color(blue)(cancel(color(black)(10^(7))))color(red)(cancel(color(black)("m"^(-1)))) * 5^2)/(5^2 + 4.348 * color(blue)(cancel(color(black)(10^(-7))))color(red)(cancel(color(black)("m"))) * 1.097 * color(blue)(cancel(color(black)(10^(7))))color(red)(cancel(color(black)("m"^(-1))))))#
#color(darkgreen)(ul(color(black)(n_2 = sqrt(4.00554) ~~ 2)))#
Therefore, you can say that the frequency of the emitted photon corresponds to an
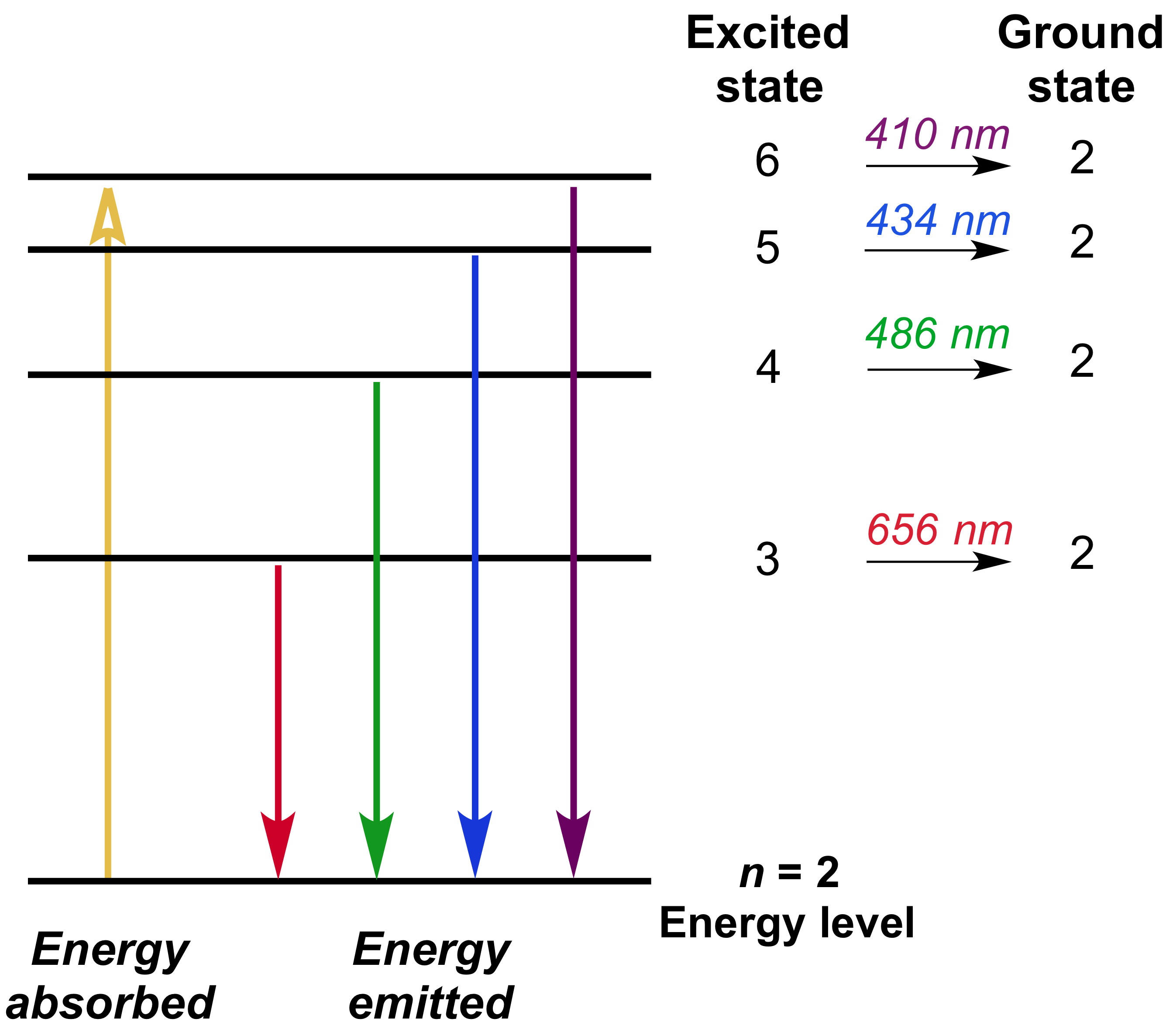
As you can see, the spectral line associated with this transition is located in the visible region of the electromagnetic spectrum, the emitted photon corresponding to the color blue.

