Question #b8186
1 Answer
See below.
Explanation:
I'll answer the 1st question, which should help you with the rest.
Otherwise you should post them as separate questions.
13.24
Arrange the 1/2 cells in order of increasing
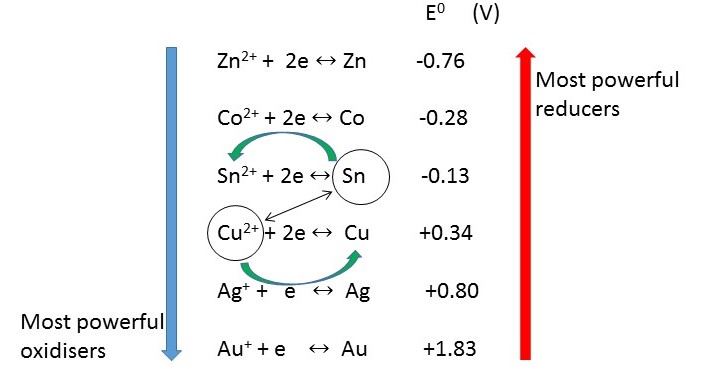
When arranged like this you can see that the most powerful oxidisers are at the bottom left of the table.
These are good at taking in electrons and tend to have more positive
The most powerful reducers are found at the top right of the table.
These are good at pushing out electrons and tend to have more negative
Note the 1/2 cells have reversible arrows to show that they can go in either direction, depending on what they are coupled with.
From the diagram you can see that the metal ion which is the weakest oxidising agent will be
By the same reasoning, you can see that the metal ion which is the strongest oxidising agent will be
The metal that is the strongest reducing agent will be
The metal that is the weakest reducing agent will
An electric current will flow between two suitably connected 1/2 cells if there is a difference in potential between them.
The 1/2 cell with the most +ve
A useful rule of thumb is the "anti - clockwise rule".
This states that any species on the left of the table can oxidise any species above it and to the right.
We say "bottom left will oxidise top right".
An equivalent statement would be "top right will reduce bottom left".
If you look at the graphic you can see that
The answer is therefore "yes".
The 1/2 cells will proceed in the direction shown by the arrows, hence the name "anti - clockwise rule".
If you were asked to find the value of
You get this by subtracting the least +ve
This should help you with the other questions.
No. Using the above rule you can see that
All the metals ions below
Any metals above
Please note that these all refer to standard conditions. Chemists often drive reactions in the direction they want by altering factors such as the pH, concentration and temperature.

