Question

How is `"CO"_2` nonpolar?

Answer 1

By symmetry.

---

Polarity is a vector concept, i.e. a bond is polar because the electric dipole moment `vecmu` points in a given direction (`x,y,z`) with a given magnitude `|vecmu|`, i.e.

`vecmu = << mu_x, mu_y, mu_z >>`

As vectors of identical magnitudes in exactly opposite directions add to cancel out completely, a "perfectly symmetrical" compound must be nonpolar, so that

`sum_i vecmu_i = 0`

For `"CO"_2`, we would have...

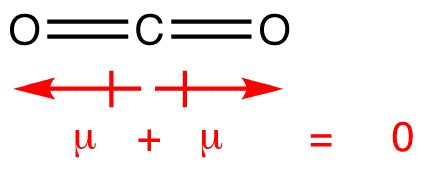http://www.ochempal.org/

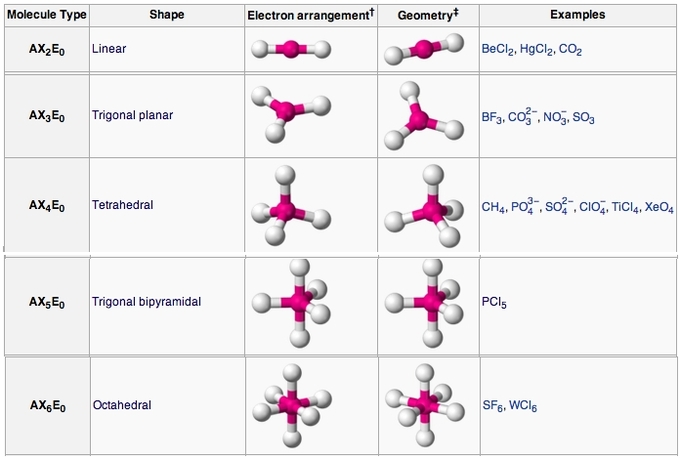
So, what do we mean by "perfectly symmetrical"? We mean the parent geometries of each so-called VSEPR structure, i.e. the ones with no lone pairs of electrons:

• two-atom linear, e.g. `"N"_2`
• three-atom linear, e.g. `"CO"_2`
• trigonal planar, e.g. `"BF"_3`
• tetrahedral, e.g. `"CCl"_4`
• trigonal bipyramidal, e.g. `"PF"_5`
• octahedral, e.g. `"SF"_6`
• etc.

all of which were NONPOLAR as listed above.

https://figures.boundless-cdn.com/

The following, more usual examples, are POLAR:

• `"NO"^(+)`, i.e. `:"N"-=stackrel((+))("O": )`, two-atom linear
• `"N"_2"O"`, i.e. `:stackrel((-))ddot"N"=stackrel((+))"N"=ddot"O":`, three-atom linear
• `"AlF"_2"Cl"`, trigonal planar
• `"CH"_3"Cl"`, tetrahedral
• `"PF"_3"Cl"_2`, trigonal bipyramidal
• `"SF"_5"Cl"`, octahedral