Question

Solve the differential equation `y'+2y=3x+1` with initial conditions `y(1) = -1` using Euler approximation ?

Answer 1

See below.

Explanation:

Making the Euler differences we have

`(y_k-y_(k-1))/h=1+3x_(k-1)-2y_(k-1)` or

`y_k=(1-2h)y_(k-1)+h(1+3x_(k-1))`. Now beginning with `x_0=1,y_0=2` and knowing that `x_k = 1+kh, k=0,1,cdots,n` we can calculate the `y_k`. Here `n=floor((2-1)/h)`

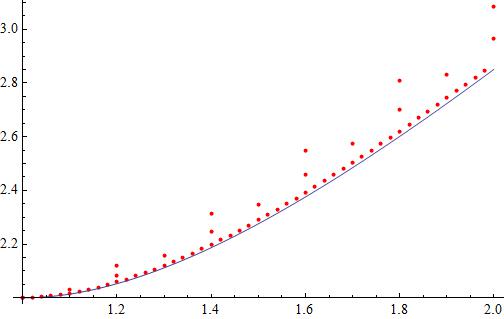
Follow a comparison between the two Euler approximations and the exact solution of the differential equation which is

`y=1/4(3e^(2(1-x))+6x-1)`

The coarser approximation is for `h=0.2` follows the approximation for `h=0.1` and also was included an approximation for `h=0.02`