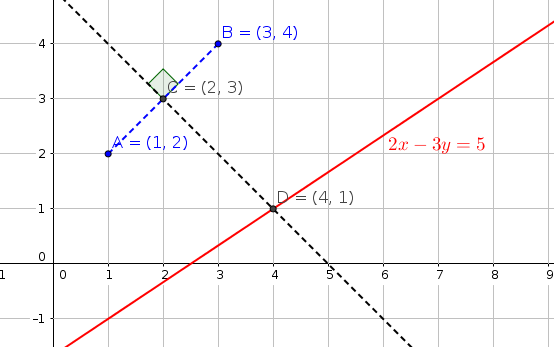
#"1-draw the points A(1,2) and B(3,4)"#
#"2-draw a line segment AB"#
#"3-find midpoint of the line segment AB"#
#C(x,y)=((1+3)/2,(2+4)/2)" , "C(2,3)#
#"4-draw a line(black and dotted) passing C(2,3) and"#
#"perpendicular to the line segment AB"#
#"since the slope of the AB is 1,the slope of the black line is -1"#
#"we can find out the equation of black dotted line."#
#y-3=-1(x-2)#
#y=-1(x-2)+3#
#y=-x+2+3#
#y=-x+5#
#x+y=5#
#"now we have two equation."#
#2x-3y=5" "(1)#
#x+y=5" "(2)#
#"let us expand the equation (2) by 3"#
#3(x+y)=3*5#
#3x+3y=15" "(3)#
#"let us sum (1) and (3)"#
#2x-cancel(3y)+3x+cancel(3y)=5+15#
#5x=20#
#x=20/5=4#
#"now use (1) or (2)"#
#x+y=5#
#4+y=5#
#y=5-4#
#y=1#

