Question

Question #93dc2

Answer 1

Consider a solid sphere of radius `R` and mass `M` as shown in the figure below

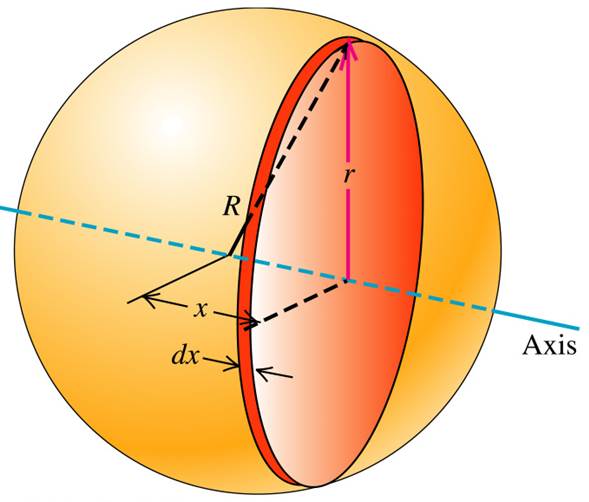cdn.miniphysics.com

We need to calculate Moment of Inertia of this sphere about its diameter along `x`-axis. The sphere can be considered to be made up of infinitesimal solid cylinders.
Consider a solid cylinder of thickness `dx` located at a distance `x` from the center of sphere. Let `r` be radius of this cylinder.
We know that moment of inertia for a solid cylinder is given by the expression

`I=1/2MR^2`

`:.` Moment of inertia of the infinitesimal cylinder is

`dI=1/2dmcdot r^2` ......(1)

`dm` can be calculated with help of density of the sphere `rho` and volume of the infinitesimal cylinder

`dm=ρcdotπr^2dx`

Substitute this value in equation (1)

`dI=1/2ρπr^4dx`

Writing `r` in terms of variable `xand R` above expression becomes

`dI=1/2ρπ(R^2–x^2)^2dx`

Integrating between limits `-R" to " R` we get

`I=1/2ρπint_(-R)^R(R^2–x^2)^2dx`
`=>I=1/2ρπint_(-R)^R(R^4–2R^2x^2+x^4)dx`
`=>I=1/2ρπ|R^4x–2R^2x^3/3+x^5/5|_(-R)^R`
`=>I=1/2ρπ|(R^4xxR–2R^2xxR^3/3+R^5/5)-(R^4(-R)–2R^2(-R)^3/3+(-R)^5/5)|`
`=>I=1/2ρπR^5(1-2/3+1/5+1-2/3+1/5)`
`=>I=1/2ρπR^5((15-10+3+15-10+3)/15)`
`=>I=1/2ρπ16/15R^5`

Density of the sphere is given by
`ρ=M/V`
`=>ρ=M/(4/3πR^3)`

Substituting in above we get

`I=1/2(M/(4/3πR^3))π16/15R^5`
`=>I=2/5MR^2`