A certain reaction follows zero-order kinetics. Suppose the reaction went to #50%# completion after #10# minutes. What percentage of completion does the reaction reach in an additional #5# minutes?
2 Answers
75%
Explanation:
"Zero order" kinetics means that the rate = k and is independent of the amount of material present. Thus, if the rate is such that the reaction is 50% complete in 10 minutes, in another 5 minutes another 25% of the overall reaction is complete - 75% of the total reaction.
The total reaction will be completed in 20 minutes.
#75%# complete.
A reaction following zero order kinetics has the rate law:
#r(t) = k[A]^0[B]^0 cdots#
and the rate is equal to the rate constant. Consequently, the rate of consumption of all the reactant(s) is a constant, and one could plot concentration
This curve would then be a straight line:
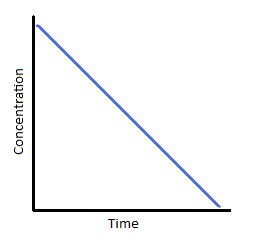
And as such, it allows us to use the reaction progress as indicative of the fraction of
Since that occurred in


