How do I calculate the force constant, zero-point energy, and the energy level spacings for #""^(12) "C"""^(16)"O"# if #tildeomega_e = "2170 cm"^-1#?
1 Answer
I got, for
#k = "1856.92 N/m"# #E_0 = 1/2hnu_0 = 2.129xx10^(-20) "J"# #DeltaE = hnu_0 = 4.258xx10^(-20) "J"#
We're treating the system as an anharmonic oscillator, which is basically two hard spheres connected by a spring, with a force constant
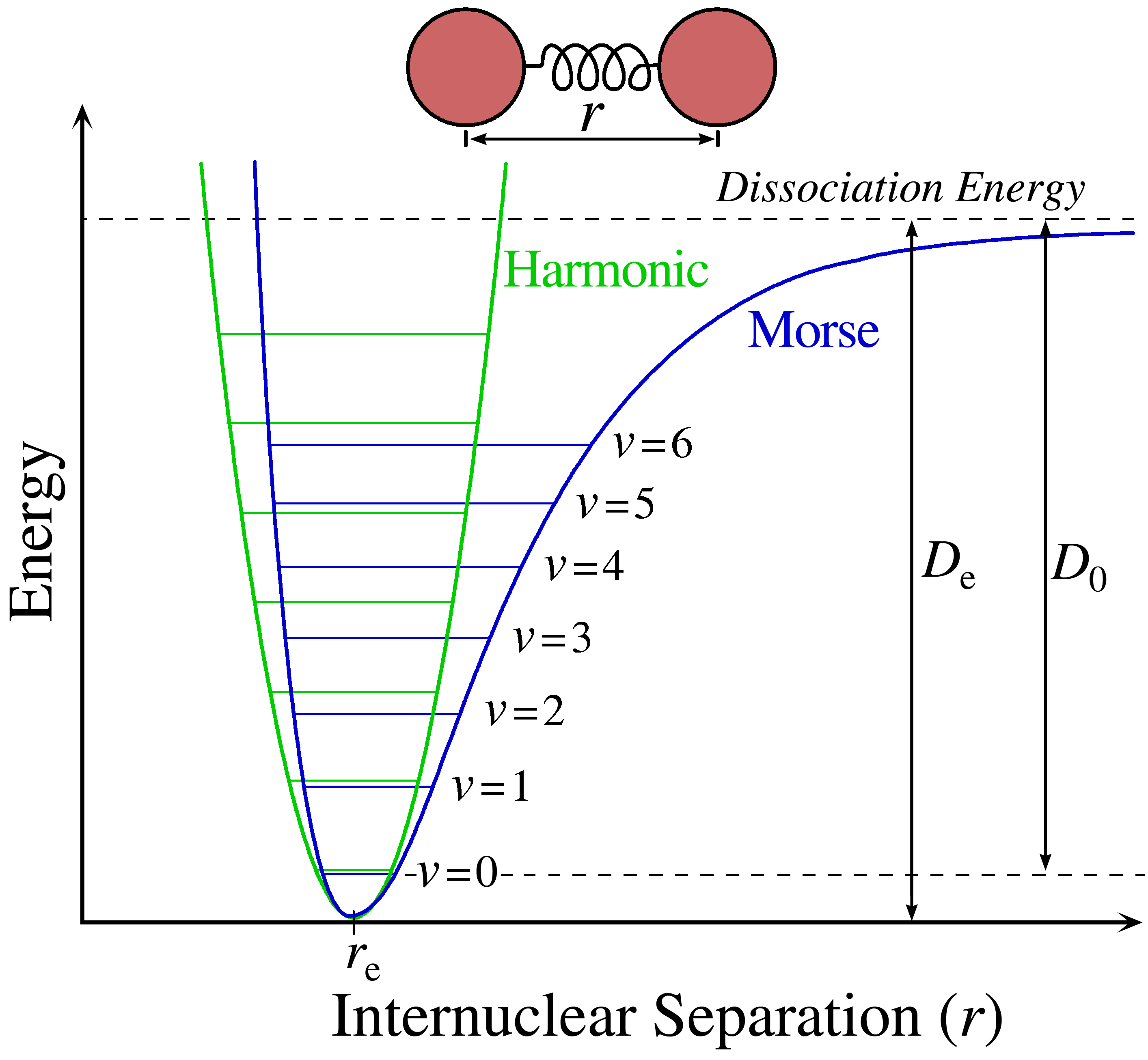
Of the above terms, zero-point energy and energy level spacings need further explanation:
#E_0# is the lowest possible energy of the molecule in its ground state, i.e. the energy#E_(upsilon)# as a function of the vibrational quantum number#upsilon# , at the energy level#upsilon = 0# .- The energy levels for this simple harmonic oscillator model go as
#bb(E_(upsilon) = hnu_0(upsilon + 1/2))# , and the energy level spacings are assumed even, because there is no dampening of this ideal spring over time.
The fundamental vibrational frequency is related to all of this, and it is the first harmonic frequency (rather than the second, third, etc. harmonics, which are the overtones) at which the molecule vibrates.
It is the frequency
Furthermore, you have actually given
#tildeomega_e -= tildenu_e = "2169.81358 cm"^(-1)# #tildeomega_echi_e -= tildenu_e chi_e = "13.28831 cm"^(-1)#
And we should recall that for an anharmonic oscillator,
#tildenu_0 = tildenu_e - 2tildenu_echi_e# .
First, convert over to
#tildenu_0 = "2170 cm"^(-1) - 2 cdot "13.28831 cm"^(-1)#
#= "2143.4 cm"^(-1)#
Then, you therefore need to convert from
#nu_0 = tildenu_0c# ,where
#c = 2.998xx10^10# #"cm/s"# is the speed of light in the proper units. If you notice,#"cm"^(-1) cdot "cm/s" = "s"^(-1)# , as required for the units of#nu_0# .
So, we obtain the fundamental vibrational frequency in the correct units so far as:
#color(green)(nu_0) = ("2143.4 cm"^(-1))(2.998xx10^10 "cm/s")#
#= color(green)(6.426xx10^13 "s"^(-1))#
So, we can now calculate the zero-point energy.
#color(blue)(E_0) = hnu_0(0 + 1/2) = 1/2hnu_0#
#= 1/2(6.626xx10^(-34) "J"cdot"s")(6.426xx10^13 "s"^(-1))#
#= color(blue)(2.129xx10^(-20) "J")#
compared to an experimental value of
Then, the energy level spacings can be calculated without much effort if we use the definition of
#color(blue)(DeltaE) = E_1 - E_0 = [ . . . ] = E_(upsilon+1) - E_(upsilon)#
#= hnu_0(upsilon + 1 + 1/2) - hnu_0(upsilon + 1/2)#
#= hnu_0(upsilon + 3/2) - hnu_0(upsilon + 1/2)#
#= hnu_0[(upsilon + 3/2) - (upsilon + 1/2)]#
#= hnu_0(cancel(upsilon) + 3/2 - cancel(upsilon) - 1/2)#
#= hnu_0#
#= (6.626xx10^(-34) "J"cdot"s")(6.426xx10^13 "s"^(-1))#
#= color(blue)(4.258xx10^(-20) "J")#
And now the last thing we need is the force constant
#omega = sqrt(k/m)# ,where
#omega# is the angular frequency and#m# is the mass.
For this system however, we instead utilize the reduced mass,
Combine that with the equation
#bb(stackrel(~)nu_0 = 1/(2pic)sqrt(k/mu))# ,
or
#bb(nu_0 = 1/(2pi)sqrt(k/mu))# .
First, we should find the reduced mass using the ISOTOPIC molar masses of each element:
#""_(8)^(16) "O":# #"15.994915 g/mol"#
#""_(6)^(12) "C":# #"12 g/mol"#
Note that in order for the units to work out, these must be in
#mu = (m_(C)m_(O))/(m_C + m_O)#
#= (("0.012000 kg/mol")("0.015994915 g/mol"))/("0.012000 + 0.015994915 kg/mol")#
#=# #"0.006856 kg/mol"#
Since we already have the value of
#2pinu_0 = sqrt(k/mu)#
#=> color(blue)(k) = mu(2pinu_0)^2#
#= "0.006856 kg"/cancel"mol"xx(cancel"1 mol")/(6.0221413xx10^(23) "things")[(2pi)(6.426xx10^13 "s"^(-1))]^2#
#=# #color(blue)("1856.92 kg/s"^2 = "1856.92 N/m")# whereas the experimental force constant in this reference is
#"1901.82 N/m"# (derived from#tildeomega_e = 2169.76689(8)# #"cm"^(-1)# , which is just another notation for#tildenu_e# ), while in this reference it is#"1860 N/m"# for#tildenu_0 ~~ "2141.42 cm"^(-1)# .

