Question

Question #4d593

Answer 1

Part (i)
graph{sqrt(sin(x)) [-5, 5, -2, 2]}

Part (ii)

Using the trapezoidal rule:

`int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}`

The values of `y=sqrt(sin(x))` are tabulated as follows (using Excel) working to 8dp

• Case (A); n=1

  

`int_0^1 \ sqrt(sin(x)) \ dx ~~ 1/2 { (0 + 0.91731727) }`
`" "= 0.5 { 0.91731727 }`
`" "= 0.45865863`

• Case (B); n=2

  

`int_0^1 \ sqrt(sin(x)) \ dx ~~ 0.5/2 { (0 + 0.91731727) + (0.69240561) }`
`" "= 0.25 { + 0.91731727 + 2(0.69240561) }`
`" "= 0.25 { + 0.91731727 + 1.38481123 }`
`" "= 0.25 { + 2.30212851 }`
`" "= 0.57553212`

• Case (B); n=4

  

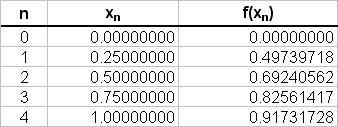
`int_0^1 \ sqrt(sin(x)) \ dx ~~ 0.25/2 { (0 + 0.91731727) +`
`" " 2(0.49739718 + 0.69240561 + 0.82561417) }`
`" "= 0.125 { 0.91731727 + 2(2.01541697) }`
`" "= 0.125 { 0.91731727 + 4.03083394 }`
`" "= 0.125 { 4.94815122 }`
`" "= 0.6185189`

• Case (B); n=8

  

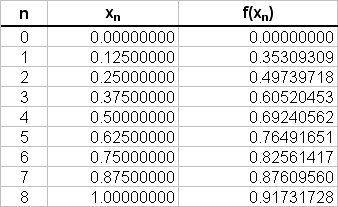
`int_0^1 \ sqrt(sin(x)) \ dx ~~ 0.125/2 { (0 + 0.91731727) +`
`" " 2(0.35309309 + 0.49739718 + 0.60520453 + 0.69240561 +`
`" " 0.76491651 + 0.82561417 + 0.8760956) }`
`" "= 0.0625 { 0.91731727 + 2(4.61472671) }`
`" "= 0.0625 { 0.91731727 + 9.22945343 }`
`" "= 0.0625 { 10.14677071 }`
`" "= 0.63417316`

• Case (B); n=16

  

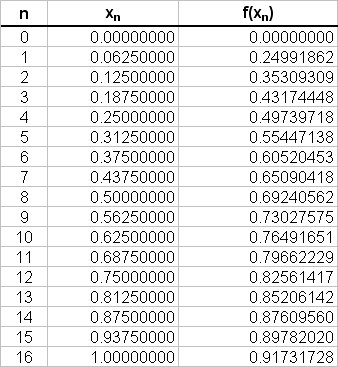
`int_0^1 \ sqrt(sin(x)) \ dx ~~ 0.0625/2 { (0 + 0.91731727) +`
`" " 2(0.24991862 + 0.35309309 + 0.43174448 + 0.49739718 +`
`" " 0.55447138 + 0.60520453 + 0.65090418 + 0.69240561 +`
`" " 0.73027575 + 0.76491651 + 0.79662229 + 0.82561417 +`
`" " 0.85206141 + 0.8760956 + 0.89782019) }`
`" "= 0.03125 { 0.91731727 + 2(9.77854504) }`
`" "= 0.03125 { 0.91731727 + 19.55709009 }`
`" "= 0.03125 { 20.47440737 }`
`" "= 0.63982523`

Part (iii)

Obviously the more strips we take the more accurate the result.

It is not the number of decimal places that the trapezium rule is calculated to that helps with accuracy, but rather the number of strips, and the last two calculations (`n=8` and `n=16`) are only consistent tow within 1 decimal place.

Based on these estimates, we can conclude that:

`int_0^1 \ sqrt(sin(x)) \ dx =0.6` (1dp)

The integral does not have an elementary solution so to compute the exact result is difficult. However, numerically it can be shown that the solution is `0.642977634658315 ...` which is consistent with our analysis