Question

Question #1e8c1

Answer 1

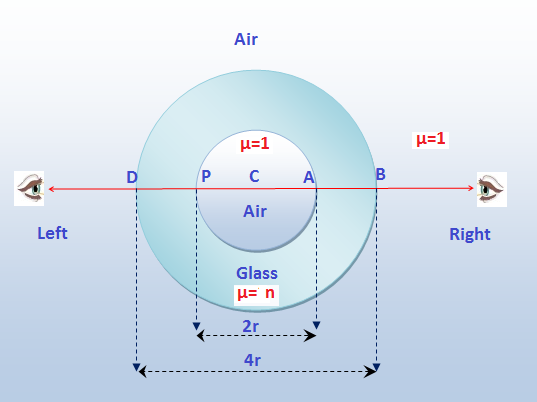
The situation as described in the question has been shown in above figure in which the black spot to be viewed is at the point P

Here we will use the following formula for refraction at curve surface to calculate the shift.

FORMULA

`color(blue)(mu_r/v-mu_i/u=(mu_r-mu_i)/R.........[1])`

Where

`mu_i->"refractive index of the medium of incident ray"`

`mu_r->"refractive index of the medium of refracted ray"`

`u->"object distance"`

`u->"image distance"`

`R->"radius of curvature of the curved refracting interface "`

When viewed from right the refraction will occur in two curved interface.
1) From `"air" to "glass"` then

`mu_i=1, " "mu_r=n," "u=-2r," "R=-r," "v=v_1(say)`

Inserting these in [1] we get

`color(green)(n/v_1-1/(-2r)=(n-1)/-r)`

`color(green)(=>n/v_1+1/(2r)=-n/r+1/r)`

`color(green)(=>n/v_1=-n/r+1/(2r)=-(2n-1)/(2r)`

`color(green)(=>v_1=-(2nr)/(2n-1)" where " n>1`

2) From `"glass" to "air"` then

`mu_i=n, " "mu_r=1," "u=-r-(2nr)/(2n-1)=-(r(4n-1))/(2n-1),`
`R=-2r," "v=v_2(say)`

Inserting these in [1] we get

`color(green)(1/v_2-n/(-(r(4n-1))/(2n-1))=(1-n)/(-2r)`

`color(green)(=>1/v_2+(n(2n-1))/(r(4n-1))=(n-1)/(2r)`

`color(green)(=>1/v_2=(n-1)/(2r)-(n(2n-1))/(r(4n-1))`

`color(green)(=>1/v_2=(4n^2-5n+1-4n^2+2n)/(2r(4n-1))`

`color(green)(=>1/v_2=-(3n-1)/(2r(4n-1))`

`color(green)(=>v_2=-(2r(4n-1))/(3n-1)`

So finally Shift of point P when viewed from right will be

`color(red)(S_R=PB-abs(v_2)=3r-abs(v_2)=3r-(2r(4n-1))/(3n-1))`

`color(red)(=>S_R=r/(3n-1)(9n-3-8n+2)`

`color(red)(=>S_R=(r(n-1))/(3n-1))`

When viewed from left the refraction will occur in one curved interface.

From `"glass" to "air only"` then

`mu_i=n, " "mu_r=1," "u=-r," "R=-2r," "v=v_3say)`

Inserting these in [1] we get

`color(blue)(1/v_3-n/-r=(1-n)/(-2r)`

`color(blue)(=>1/v_3+n/r=-1/(2r)+n/(2r)`

`color(blue)(=>1/v_3=-1/(2r)+n/(2r)-n/r`

`color(blue)(=>1/v_3=-1/(2r)(1-n+2n)`

`color(blue)(=>v_3=-(2r)/(n+1)`

So finally Shift of point P when viewed from left will be

`color(red)(S_L=PD-abs(v_3)=r-abs(v_3)=r-(2r)/(n+1)=(r(n-1))/(n+1))`