A percentile is a location in a distribution that has a specified amount (or percentage) of the distribution "below it" (to its left). In other words, if the #n^"th"# percentile is #x#, and we draw a random number #X# from the distribution, then the chance of #X# being less than #x# is #n %#:
#n^"th" " percentile" = x" "#means#" " P(X < x)=n%.#
For example, in a standard normal curve (with #mu = 0# and #sigma = 1#), the point where #x=0# (i.e. the #y#-axis) is the 50th percentile, because 50% of the curve's area falls to the left of #x=0#:

The standard normal distribution #Z# is such a good baseline, we actually have a table of values designed specifically for looking up percentiles for this curve. It's called a #z#-table, and it looks something like this:
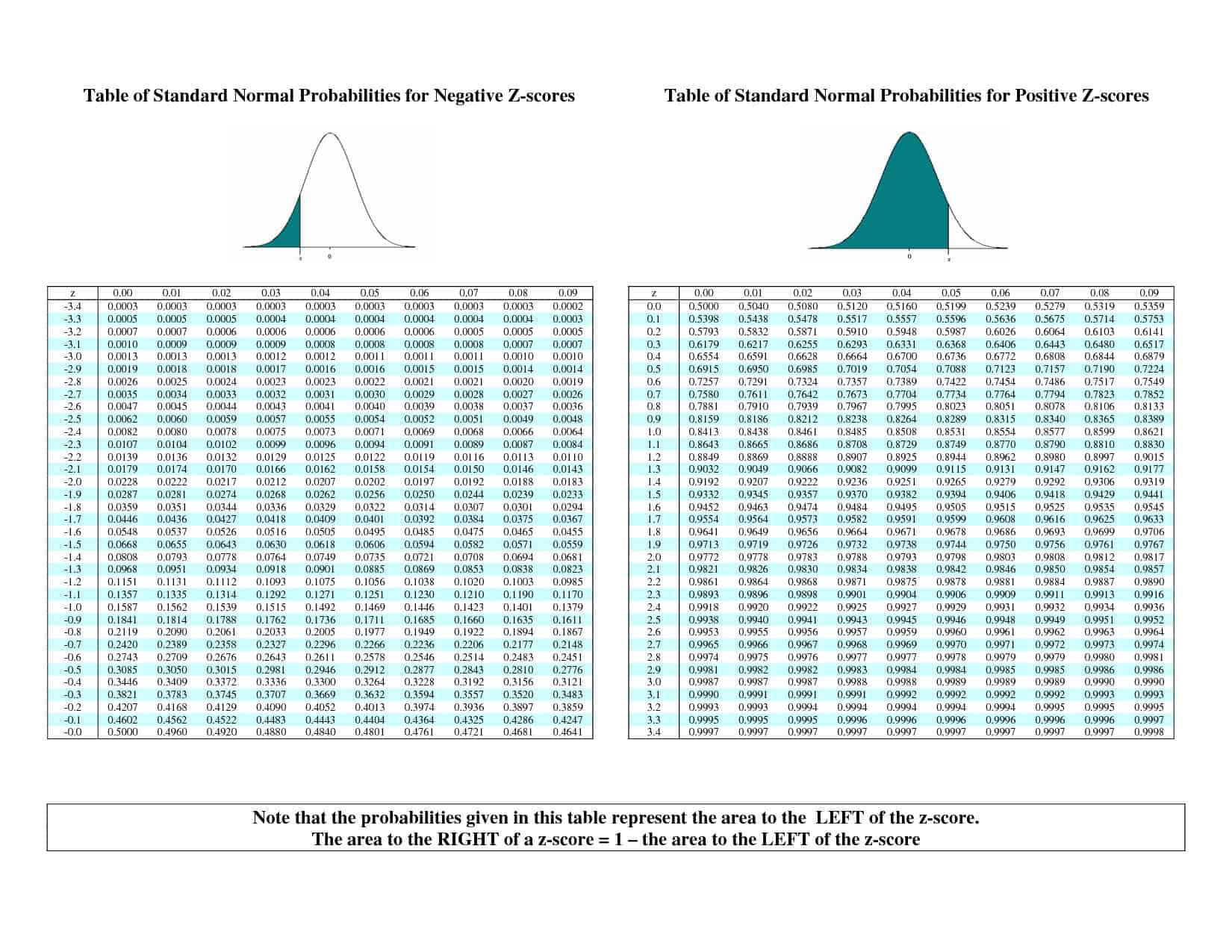
How do we use it? Let's say we want the 25th percentile for the standard normal distribution. We find the value closest to 0.25 in the table (which happens to be 0.2514) and see that it's in row #"-"0.6# and column #0.07#. For this table, that means the 25th percentile is (approximately) #"-"0.67#.
But wait—how does that help when we want a percentile for any normal distribution #X#? We need to find a connection between any curve and the standard normal curve. That connection is found by shifting the #X# distribution left-to-right so that it's centered at #0#, and then stretching/squishing it so that its standard deviation is #1#. The formula for this is:
#Z=(X-mu)/sigma#
where #mu# is the mean of #X# and #sigma# is the s.d. of #X#.
If we know the percentile we want from the #Z# distribution, we can solve for #X# by rearranging the equation into
#X=sigma Z + mu#.
As an example, let's use the first question you asked, where #X# is normally distributed with #mu = 81.2# and #sigma = 12.4#, and we seek the 16th percentile.
From the table above, the 16th percentile from the #Z# distribution is approximately #"-"0.99#. The equivalent location in our #X# distribution is then:
#X=(12.4)("-"0.99)+81.2#
#color(white)X="-"12.276+81.2#
#color(white)X=68.924#
What this says is: if #X# is a normal curve with #mu=81.2 " feet"# and #sigma = 12.4 " feet"#, then there is a 16% chance of an observation from #X# being less than #68.924 " feet"#.
I'll leave the rest for you as an exercise; with the formulas above, it shouldn't be that hard.
Hope this helps!



