It maybe caused in two ways depending on how the incident ray is made to fall on the mirror.
Case-I When the ray is incident at an angle #30^@ " above"# the horizontal.
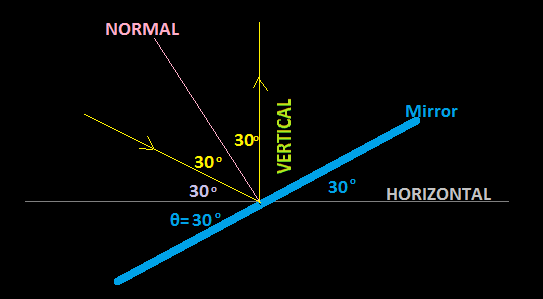
Let the angle be #theta^@#with which the mirror to be placed with the horizontal so as to reflect vertically the ray incident on the mirror at #30^@# with the horizontal.
Incident ray is inclined at angle #30^@# (above) with the horizontal and reflected ray is vertical. So the angle between reflected ray and incident ray may be #(90^@-30^@)=60^@# Hence angle of incidence will be #=1/2xx60^@=30^@#
So it is obvious that
#theta+30^@+30^@=90^@#
#=>theta =30^@#
Case-II When the ray is incident at an angle #30^@ " below"# the horizontal.
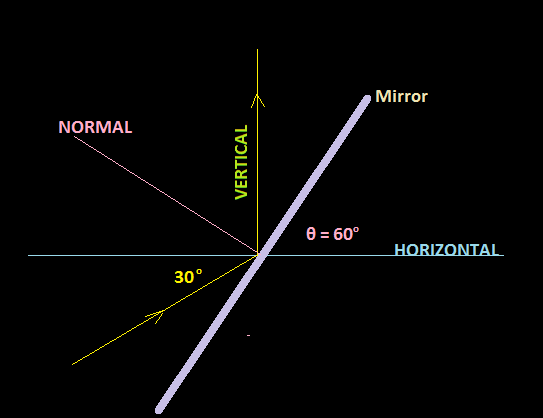
In this case if mirror makes an angle #theta# to reflect the incident ray in vertical direction, then the vertical reflected ray will make #(90-theta)^@# with the mirror.
So the angle of reflection becomes #(90^@-(90-theta)^@)=theta^@#
But the incident ray makes an angle #30^@# below the horizontal. So it makes an angle #(90^@+30^@)=120^@#with the vertical reflected ray and as a result the angle of incidence or the angle of reflection becomes #1/2xx120^@=60^@#
So we have #theta=60^@#



