A schematic cooling curve for benzene is shown below.
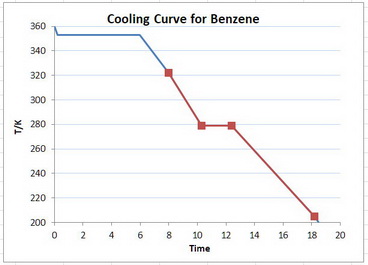
You are starting with the liquid at the top of the red graph, cooling it to its freezing point, freezing the liquid along the horizontal line, and then cooling the solid to bottom of the red graph.
Thus, there are three separate heat removals involved in this problem:
- #q_1# = heat removed by cooling the liquid from 322 K to 279 K
- #q_2# = heat removed by freezing the liquid at 279 K
- #q_3# = heat removed by cooling the solid from 279 K to 205 K
#q = q_1 + q_2 + q_3 = mC_text(liq)ΔT_1 + nΔ_text(melt)H + mC_text(sol)ΔT_3#
where
#mcolor(white)(ml) = "the mass of the sample"#
#Ccolor(white)(ml) = "the specific heat capacity of benzene"#
#ΔTcolor(white)(l) = T_"f" -T_"i"#
#bbq_1#
#ΔT_1 = "279 K - 322 K = -43 K"#
#q_1 = mC_text(liq)ΔT = 50.4 color(red)(cancel(color(black)("g"))) × 1.73 color(white)(l)"J"·color(red)(cancel(color(black)( "K"^"-1""g"^"-1"))) × ("-43" color(red)(cancel(color(black)("K")))) = "-3749 J" = "-3.749 kJ"#
#bbq_2#
#n = 50.4 color(red)(cancel(color(black)("g"))) × "1 mol"/(78.11 color(red)(cancel(color(black)("g")))) = "0.6452 mol"#
#q_2 = nΔ_text(melt)H = 0.6452 color(red)(cancel(color(black)("mol"))) × ("-9.8 kJ"·color(red)(cancel(color(black)("mol"^"-1")))) = "6.32 kJ"#
#bbq_3#
#ΔT_1 = "205 K - 279 K = -74 K"#
#q_1 = mC_text(sol)ΔT = 50.4 color(red)(cancel(color(black)("g"))) × 1.5 color(white)(l)"J"·color(red)(cancel(color(black)( "K"^"-1""g"^"-1"))) × ("-74" color(red)(cancel(color(black)("K")))) = "-5590 J" = "-5.59 kJ"#
#q = q_1 + q_2 + q_3 = "-3.749 - 6.32 - 5.59) kJ" = "-15.7 kJ"#
The process releases 15.7 kJ of heat energy.


