A typical heating curve for a compound like #"SO"_2# is shown below.
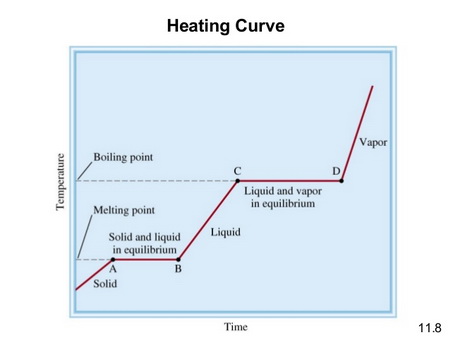
(From SlideShare)
The melting point of #"SO"_2# is -73.15 °C (200.00 K), and the boiling point is -10.0 °C (263.1 K).
In this problem, we are starting with the liquid at point B , warming it to its boiling point C, and then evaporating it to point D.
Thus, there are two separate heat transfers involved:
- #q_1# = heat required to warm the liquid from from 200.5 K to 263.1 K (Point B to C in the diagram)
- #q_2# = heat required to evaporate the liquid at 263.1 K (Point C to D)
#q = q_1 + q_2 = mCΔT + nΔ_text(vap)H#
where
#q_1# and #q_2# are the heats involved in each step
#mcolor(white)(ml) = "the mass of the sample"#
#Ccolor(white)(ml) = "the specific heat capacity of SO"_2 = "1.36 J·°K"^"-1""g"^"-1"#
#ΔTcolor(white)(l) = T_"f" -T_"i"#
#Δ_text(fus)H = "the molar enthalpy of evaporation of SO"_2 = "24.9 kJ·mol"^"-1"#
#bbq_1#
#ΔT = "263.1 K - 200.5 K" = "62.6 K"#
#q_1 = mCΔT = 95.1 color(red)(cancel(color(black)("g"))) × 1.36 color(white)(l)"J"·color(red)(cancel(color(black)( "K"^"-1""g"^"-1"))) × 62.6 color(red)(cancel(color(black)("K"))) = "8096 J" = "8.096 kJ"#
#bbq_2#
#n = 95.1 color(red)(cancel(color(black)("g SO"_2))) × "1 mol SO"_2/(64.06 color(red)(cancel(color(black)("g SO"_2)))) = "1.485 mol SO"_2#
#q_2 = 1.485 color(red)(cancel(color(black)("mol"))) × "24.9 kJ"·color(red)(cancel(color(black)("mol"^"-1"))) = "36.97 J"#
#q = q_1 + q_2 = "(8.096 + 36.97) kJ" = "45.1 kJ"#
The process requires 45.1 kJ of heat energy.


